Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1 2

 

#1 02. 03. 2012 11:20

Petra20
Příspěvky: 60
Reputace:   0 
 

integrace goniometrických funkcí

Mám zadáno $\int(sin x * cos x)/(1+sin^4 x)dx . Mám ještě zadánou substituci: a)sin x=t, b)tg x=t. Znám výsledek buď : 1/2arctg(1+tg^2 x), nebo  ½ arctg(sin^2 x). Potřebuji vědět jak se k tomu dojde. něco jsem zkoušela, ale nevím, z čeho např dostanu tg^2 x. Díky moc za pomoc

Offline

  • (téma jako vyřešené označil(a) jelena)

#2 02. 03. 2012 13:24

Honzc
Příspěvky: 4616
Reputace:   245 
 

Re: integrace goniometrických funkcí

↑ Petra20:
Zcela rozhodně použij
1. substituci 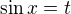$\sin x=t$  ($\cos x \;dx=dt$) a potom ještě
2.substituci $t^{2}=u$ ($t\;dt=\frac{du}{2}$)

Autor skryl část textu. Zobrazit/skrýt!

Offline

 

#3 02. 03. 2012 13:48

Petra20
Příspěvky: 60
Reputace:   0 
 

Re: integrace goniometrických funkcí

a jak se to bude resit pres tg x=t ?

Offline

 

#4 02. 03. 2012 13:54 — Editoval kaja.marik (02. 03. 2012 13:55)

kaja.marik
Veterán
Příspěvky: 1915
Reputace:   57 
 

Re: integrace goniometrických funkcí

↑ Petra20:
sin(x)=t/sqrt(1+t^2), cos(x)=1/sqrt(1+t^2), dx=dt/(1+t^2)

Offline

 

#5 02. 03. 2012 14:49

vanok
Příspěvky: 14600
Reputace:   742 
 

Re: integrace goniometrických funkcí

↑ Petra20:
tu mas zaujimave substitucie
http://fr.wikipedia.org/wiki/R%C3%A8gles_de_Bioche
Iste to aj bez slovnika pochopis ... ale to vediet ti zjednodusi zivot

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

#6 02. 03. 2012 14:56

Petra20
Příspěvky: 60
Reputace:   0 
 

Re: integrace goniometrických funkcí

zkousim tu integraci pomoci sin x =t a ted mi vysel integral t/(1+t^4) dt. a ted nevim, kdyz pouziji tu druhou substituci, tak co mi z toho vznikne. me vyslo integral (odmocnina z u/(1+u^2)) * du/2t. ted nevim co stim..

Offline

 

#7 02. 03. 2012 15:06

vanok
Příspěvky: 14600
Reputace:   742 
 

Re: integrace goniometrických funkcí

↑ Petra20:
nekontroloval som to
ale pripominam ze mas
$t^4+1=(t^2+ \sqrt2 t+1)(t^2-\sqrt2 t+1)$

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

#8 02. 03. 2012 15:12

Alkac
Příspěvky: 181
Reputace:   10 
 

Re: integrace goniometrických funkcí

Lepsi substituovat t^2=s, t^4 = s^2 a ds=2tdt

Offline

 

#9 02. 03. 2012 15:13

Petra20
Příspěvky: 60
Reputace:   0 
 

Re: integrace goniometrických funkcí

a jak mi to pomuze? ja potrebuji spis vedet, jestli jsem to takto vyjadrila dobre.

Offline

 

#10 02. 03. 2012 15:17 — Editoval vanok (02. 03. 2012 15:20)

vanok
Příspěvky: 14600
Reputace:   742 
 

Re: integrace goniometrických funkcí

↑ Petra20:
urob rozklad na jednoduche zlomky
Ale ta substitucia co ti radi kolega je rychlejsia cesta

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

#11 02. 03. 2012 15:19

Petra20
Příspěvky: 60
Reputace:   0 
 

Re: integrace goniometrických funkcí

↑ Alkac: diky. zkusim to

Offline

 

#12 02. 03. 2012 15:23

Petra20
Příspěvky: 60
Reputace:   0 
 

Re: integrace goniometrických funkcí

↑ vanok: stale to nechapu. pokud si to takto rozlozim vyskace mi tam toho mnohem vic.

Offline

 

#13 02. 03. 2012 15:32

vanok
Příspěvky: 14600
Reputace:   742 
 

Re: integrace goniometrických funkcí

↑ Petra20:
tu mas kontrolu
( pozor,dal som x miesto t)
http://www.wolframalpha.com/input/?i=x%2F%28+x^4%2B1%29

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

#14 02. 03. 2012 15:36

Petra20
Příspěvky: 60
Reputace:   0 
 

Re: integrace goniometrických funkcí

a kdyz to budu delat pres tu substituci pomoci u=t^2 du=2t dt vyslo mi http://forum.matweb.cz/upload3/img/2012-03/98938_Bez%2Bn%25C3%25A1zvu.png

Offline

 

#15 02. 03. 2012 15:37

Petra20
Příspěvky: 60
Reputace:   0 
 

Re: integrace goniometrických funkcí

nevim co s tou odmocninou..

Offline

 

#16 02. 03. 2012 15:51

vanok
Příspěvky: 14600
Reputace:   742 
 

Re: integrace goniometrických funkcí

↑ Petra20:
spatne si nahradila
ten citatel je 1.du
ten zvysok tam nepatri.

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

#17 02. 03. 2012 15:59

Petra20
Příspěvky: 60
Reputace:   0 
 

Re: integrace goniometrických funkcí

↑ vanok: promin, ale co je to zvysok? vyjadreni by vlastne bylo du/t

Offline

 

#18 02. 03. 2012 16:31

vanok
Příspěvky: 14600
Reputace:   742 
 

Re: integrace goniometrických funkcí

no je to ozaj jednoduche
ten zlomok v integraly je 1/(1+s^2)

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

#19 02. 03. 2012 16:36

Petra20
Příspěvky: 60
Reputace:   0 
 

Re: integrace goniometrických funkcí

t se mi vyrusilo? a 1/2 dam pred integral?

Offline

 

#20 02. 03. 2012 16:49

vanok
Příspěvky: 14600
Reputace:   742 
 

Re: integrace goniometrických funkcí

↑ Petra20:,
ano a bude to dokonale.
A na konci, nezabudni sa vratit, k "neznamej " x

Inac ta druha metoda,  co som pisal je ozaj dlhsia...

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

#21 02. 03. 2012 22:11

Petra20
Příspěvky: 60
Reputace:   0 
 

Re: integrace goniometrických funkcí

ted zkousim tu druhou variantu, kdy mam tg x=t. dosadila jsem vse ale nevim,jak to mam dal upravit, aby mi to nejak rozumne vyslo. Zkousela jsem to i roznasobovat, ale z toho jsem uz nic dalsiho nedostala. http://forum.matweb.cz/upload3/img/2012-03/22591_Bez%2Bn%25C3%25A1zvu15.png

Offline

 

#22 02. 03. 2012 22:37

kaja.marik
Veterán
Příspěvky: 1915
Reputace:   57 
 

Re: integrace goniometrických funkcí

↑ Petra20:
v tom jmenovateli spatne umocnujete na ctvrtou

Offline

 

#23 03. 03. 2012 08:26

Petra20
Příspěvky: 60
Reputace:   0 
 

Re: integrace goniometrických funkcí

a jak by to teda bylo?

Offline

 

#24 03. 03. 2012 08:38

Honzc
Příspěvky: 4616
Reputace:   245 
 

Re: integrace goniometrických funkcí

↑ Petra20:
Úplně nejelegantnější substituce u tohoto příkladu je"
$\sin ^{2}x=t, \sin x\cdot\cos x\cdot dx=\frac{1}{2}dt$

Offline

 

#25 03. 03. 2012 08:40

Petra20
Příspěvky: 60
Reputace:   0 
 

Re: integrace goniometrických funkcí

ja vim, jenze ja mam ty substituce zadane. pres tuto uz jsem to delala a jednoduse vyresila. nyni potrebuju pres tg x=t

Offline

 

 

Stránky: 1 2

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson