Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 03. 2012 17:32
nerozumiem ulohe
Zdravim Vas, nasiel som jednu ulohu s minulorocnej maturity a nerozumiem zadaniu ktore znie:
Urcte korene rovnice cos x = cos 12 stupnov z intervalu zobacikova zatvorka - 90 stupnov ; 360 stupnov koniec zobacikovej zatvorky. Do odpovedoveho harka zapiste sucet korenov tejto rovnice z daneho intervalu.
Ospravedlnujem sa za zobacikove zatvorky ale neviem ako inac by som to zapisal. Viem ze tu mate na to ten jazyk ale ja ho neovladam.
Kokos a nerozumiem tomu absolutne, ved ked je na oboch stranach rovnaka operacie tak sa to rovna 12 stupnov nie? To je taka uloha akoby som sa opytal 2^10 = x^10 a comu sa rovna x ?? Ved tam nic ine nesedi.. alebo log 1000 = log x comu sa rovna x ? No predsa 1000 nie?? Prosim pomozte niekto vopred dakujem !!!
Offline
#5 05. 03. 2012 17:47 — Editoval brodzko (05. 03. 2012 17:49)
Re: nerozumiem ulohe
Nie, Hanisova rovnica bude mať dve riešenia, 2 a -2 :) Tak isto tvoja rovnica bude mať riešení niekoľko - pri riešení goniometrických rovníc musíš uvažovať 4 sektory: v I. sektore je koreňom 12°, v II. sektore 180-12, v III. 180+12 a vo IV. 360-12. Chyták je v tom, že hľadáš korene len z určitého intervalu - tieto si nájdeš, spočítaš a vyriešené :)
Edit: Ešte som pozabudol na to, že každá goniometrická f-cia má v každom sektore svoje význačné znamienka, ktoré musíš uvážiť tiež :) pri cos sú to konkrétne v poradí I II III IV: + - - + - tebe teda vyhovujú len dva sektory, rozumieš ktoré?
Nezabudnite navštíviť MatPhys - môj blog o teórii a myšlienkach z matematiky a fyziky.
Offline
#7 05. 03. 2012 17:53
Re: nerozumiem ulohe
↑ Matej1117:
Ahoj,
Matej1117 napsal(a):
Ospravedlnujem sa za zobacikove zatvorky ale neviem ako inac by som to zapisal. Viem ze tu mate na to ten jazyk ale ja ho neovladam.
máš na klávesnici tyto klávesy?
Znaky < a > napíšeš pomocí nich.
Offline
#8 05. 03. 2012 17:53 — Editoval Hanis (06. 03. 2012 09:38)
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: nerozumiem ulohe
↑ brodzko: Ach jo, člověk se tu snaží o Sokratovský dialog a ty mi tu do toho vpadneš.
Načrtni si graf funkce cos v intervale <-pi/2;2pi>, vyznač přibližně cos 12° a koukni, jestli někde cos nemá náhodou stejnou funkční hodnotu...
Jinak ↑ brodzko: má pravdu.
Offline
#9 05. 03. 2012 17:55
Re: nerozumiem ulohe
Mne to vychádza po súčte 348°. Ak si totiž nakreslíš priebeh funkcie kosínus v zadanom intervale, nájdeš vyhovujúce korene -12°; 12°; 348°. Skús si to všetko nakresliť, snáď pomohlo :)
Nezabudnite navštíviť MatPhys - môj blog o teórii a myšlienkach z matematiky a fyziky.
Offline
#17 06. 03. 2012 13:57
Re: nerozumiem ulohe
↑ Matej1117:
Potřebuješ vědět, že  právě když existuje celé číslo
právě když existuje celé číslo  takové, že buďto
takové, že buďto  nebo
nebo  .
.
Ve stupních: právě když existuje celé číslo
právě když existuje celé číslo  takové, že buďto
takové, že buďto  nebo
nebo  .
.
Podívej se na graf funkce cos a ujisti se, že to tak opravdu je.
Offline
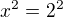 kolik to má řešení?
kolik to má řešení?
