Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 03. 2012 14:43
- Michalowic

- Zelenáč
- Příspěvky: 5
- Reputace: 0
Inverzní matice
Zdravím,
k výpočtu maticové rovnice A * X = B je třeba inverzní matice A. Při jejím výpočtu se ale vždy dostanu do slepé uličky a nevím co s ní. Pomůže někdo?
matice A je:
1 2 -3
3 2 -4
2 -1 0
Potřebuji tedy spočítat inverzní matici 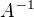 . Nejlépe i s popsanými kroky (který řádek je násoben jakým číslem apod.)
. Nejlépe i s popsanými kroky (který řádek je násoben jakým číslem apod.)
Předem moc děkuji za pomoc!
Offline
#2 21. 03. 2012 17:10 — Editoval Andrejka3 (21. 03. 2012 17:14)
Re: Inverzní matice
↑ Michalowic:
Ahoj.
Označme sloupce inverzní matice jako 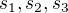 .
.
Platí , kde
, kde  je jednotková matice 3x3, tj. jedničky na hlavní diagonále, jinde nuly.
je jednotková matice 3x3, tj. jedničky na hlavní diagonále, jinde nuly.
Rovnice výše lze rozepsat: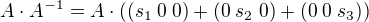 , kde napr.
, kde napr. 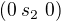 je matice 3x3, jejíž krajní sloupce jsou nulové a prostřední je
je matice 3x3, jejíž krajní sloupce jsou nulové a prostřední je 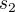 . Můžeme dále pokračovat využitím distributivity
. Můžeme dále pokračovat využitím distributivity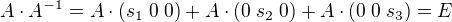 , přičemž nyní je patrné, že
, přičemž nyní je patrné, že
první součin na levé straně, tj. 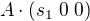 má na svědomí pouze první sloupec matice
má na svědomí pouze první sloupec matice  ,
,
druhý součin na levé straně, tj.  , má na svědomí pouze 2. sloupec matice
, má na svědomí pouze 2. sloupec matice  ,
,
treti...
Tedy se problém redukuje na řešení tří soustav lineárních rovnic: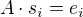 pro
pro  . Kde
. Kde 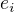 je
je  -tý sloupec jednotkové matice.
-tý sloupec jednotkové matice.
Řešit soustavy lineárních rovnic, předpokládám, umíš.
Tady je výhoda, že je můžeme řešit najednou.
Napíšeme a Gaussovou eliminací převedeme na tvar
a Gaussovou eliminací převedeme na tvar 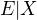 , kde porovnáním s předchozím je vidět, že
, kde porovnáním s předchozím je vidět, že  -tý sloupec matice
-tý sloupec matice  je roven
je roven  , tj. vpravo máme rovnou inverzní matici.
, tj. vpravo máme rovnou inverzní matici.
Dokážeš tento postup aplikovat?
edit: snaž se napsat kroky ty, upozorním na případné chyby.
What does a drowning number theorist say?
'log log log log ...'
Offline
#3 21. 03. 2012 17:25
- Michalowic

- Zelenáč
- Příspěvky: 5
- Reputace: 0
Re: Inverzní matice
↑ Andrejka3:
Díky za příspěvek. Tvůj postup částečně chápu, ale nějak ho neumím aplikovat a nejsem si jistý, jestli je to zrovna to, co potřebuji.
Tu inverzní matici potřebuji vyřešit právě pomocí Gaussovy el. metody, což je pro mne kámen úrazu. Pokusím se popsat můj postup, vycházím z postupu probíraného na cvičení ve škole.
Můj postup je zatím takovýto:
1 2 -3 | 1 0 0
3 2 -4 | 0 1 0
2 -1 0 | 0 0 1
první řádek * -3 přičtu ke druhému
první řádek * -2 přičtu ke třetímu .. tím dostávám
1 2 -3 | 1 0 0
0 -4 5 | -3 1 0
0 -5 6 | -2 0 1
Dále jsem zkoušel prohazovat 2. a 3. řádek, násobit zlomkem apod. ale vždy jsem se dostal ke špatným číslům. Byl bych tedy rád za nakopnutí k dalšímu postupu...
btw: Omlouvám se, že matice píšu takto "textově", ale zatím jsem nějak nepronikl do syntaxe zápisu v "grafické" podobě.
Offline
#4 21. 03. 2012 17:30 — Editoval Andrejka3 (21. 03. 2012 17:35)
Re: Inverzní matice
Teď bych provedla:
-1 násobek posledního řádku přičíst k druhému. Může se to zdát zbytečné, možná i je, ale dostanu tak v druhém jedničku.
Jedničky jsou nejhezčí. Dělala bych je hned od začátku. Ale prosím takto se nespleteme.
Mě to tedy vyjde pak takto:
1 2 -3 | 1 0 0
0 1 -1| -1 1 -1
0 -5 6 | -2 0 1
Raději zkontroluj. Teď nám nezbývá než 5*druhý přičíst k třetímu.
Edit: očekávám, že provedeš navrhovanou operaci.
What does a drowning number theorist say?
'log log log log ...'
Offline
#5 21. 03. 2012 17:39
Re: Inverzní matice
↑ Michalowic:,
Tvoj zacaty postup je dobry,
normalne sa pokracuje tak ze cela prva strana matice sa transformuje na jednotkovu.
tym si skoncil prvu etapu, tak pokracuj!
druha etapa:
v poslednej matici vyraze vydel druhy riadok -4my
tretia etapa
v dalsej etape k tretiemu riadku pripocitas 5*druhy
stvrta etapa
....
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 21. 03. 2012 17:41
Re: Inverzní matice
↑ Michalowic:,
Tvoj zacaty postup je dobry,
normalne sa pokracuje tak ze cela prva strana matice sa transformuje na jednotkovu.
tym si skoncil prvu etapu, tak pokracuj!
druha etapa:
v poslednej matici vyraze vydel druhy riadok -4my
tretia etapa
v dalsej etape k tretiemu riadku pripocitas 5*druhy
stvrta etapa
....
Ahoj ↑ Andrejka3:,
zasa spolu piseme.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 21. 03. 2012 17:52
- Michalowic

- Zelenáč
- Příspěvky: 5
- Reputace: 0
Re: Inverzní matice
↑ Andrejka3:
Díky, já jsem se pořád soustředil na přičítání násobků řádků "zezhora dolu" a obráceně mě to nenapadlo.
Takže jsem pokračoval
1 2 -3 | 1 0 0
0 1 -1| -1 1 -1
0 -5 6 | -2 0 1
poté přičetl pětinásobek druhého ke třetímu (jak jsi psala)
1 2 -3 | 1 0 0
0 1 -1 | -1 1 -1
0 0 1 | -7 5 -4
poté přičetl třetí ke druhému
1 2 -3 | 1 0 0
0 1 0 | -8 6 -5
0 0 1 | -7 5 -4
poté přičetl k prvnímu třínásobek třetího
1 2 0 | -20 15 -12
0 1 0 | -8 6 -5
0 0 1 | -7 5 -4
a v posledním -2* druhý řádek k prvnímu. A to je vlastně výsledek :)
1 0 0 | -4 3 -2
0 1 0 | -8 6 -5
0 0 1 | -7 5 -4
Takže moc děkuji za pomoc, jinak bych se opravdu dál nehnul...
Offline
#8 21. 03. 2012 17:56
Re: Inverzní matice
↑ Michalowic:
Rádo se stalo.
Zdravím kolegu ↑ vanok: :)
Jinak, ze zkušenosti doporučuji se snažit vyrábět jedničky a tím dostávat co nejmenší čísla.
Ať se daří.
A.
What does a drowning number theorist say?
'log log log log ...'
Offline
#9 21. 03. 2012 18:13
- jakub.solc

- Zelenáč
- Příspěvky: 14
- Reputace: 3
Re: Inverzní matice
Dá se postupovat ještě jinak: Řádkové úpravy odpovídají násobení nějakou maticí zleva.
Inv. matici označíme L. Pokud při úpravách přejde (A|E) na (E|L), pak (A|B) přejde stejnými úpravami na (E|LB), přičemž LB je vlastně X.
Takže stačí dát doprava B a vyjde rovnou řešení X. Postup funguje dokonce i pro singulární matici A (pokud soustavu správně dořešíme).
Offline