Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Neizomorfní grupy mající stejný počet prvků všech řádů (TOTO TÉMA JE VYŘEŠENÉ)
#1 27. 03. 2012 18:35 — Editoval Andrejka3 (27. 03. 2012 18:44)
Neizomorfní grupy mající stejný počet prvků všech řádů
Ahoj.
Mám příklad:
Najděte dvě grupy konečného řádu, které nejsou izomorfní a mají stejný počet prvků všech řádů.
Existují vůbec takové?
Možná tomu není dobře rozumět, tak ještě trochu těžkopádněji:
Označme pro nějaké přirozené n a nějakou (konečnou) grupu G  .
.
Hledám takové dvě neizomorfní, konečné grupy G,H, že 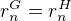 pro každé přirozené n.
pro každé přirozené n.
Pozorování: Musí být  .
.
Nemohou být obě komutativní, jinak by byly izomorfní - to, myslím, plyne z důkazu Frobenius-Stickelberger věty (klasifikace konečných komutativních grup). viz též lemma 1.64 ve skriptech.
Prosím,
máte někdo nějaký nápad?
Jinak, jde o příklad 134 ze sbírky.
edit: link na sbírku.
What does a drowning number theorist say?
'log log log log ...'
Offline
- (téma jako vyřešené označil(a) Andrejka3)
#2 28. 03. 2012 20:56
Re: Neizomorfní grupy mající stejný počet prvků všech řádů
↑ Andrejka3:
Přijde mi to jako docela zajímavá otázka, zda uvedená podmínka stačí na existenci izomorfismu.
Zkusím si projít pár konečných grup a třeba budu mít štěstí a na něco narazím (pochybuju :D).
What does a drowning number theorist say?
'log log log log ...'
Offline
#3 28. 03. 2012 21:05 — Editoval ruamaixanh (28. 03. 2012 21:06)
- ruamaixanh

- Místo: Tachov
- Příspěvky: 100
- Reputace: 11
Re: Neizomorfní grupy mající stejný počet prvků všech řádů
Zdravím,
takové grupy opravdu existují, například grupa 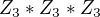 a druhá grupa je grupa matic s
a druhá grupa je grupa matic s  na diagonále,
na diagonále,  pod diagonálou a jiné prvky jsou ze
pod diagonálou a jiné prvky jsou ze 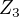 . Obě grupy mají exponent 3, ale jedna je abelovská, kdežto druhá není, tzn. nejsou izomorfní.
. Obě grupy mají exponent 3, ale jedna je abelovská, kdežto druhá není, tzn. nejsou izomorfní.
Offline
#4 28. 03. 2012 21:11
Re: Neizomorfní grupy mající stejný počet prvků všech řádů
↑ ruamaixanh:
Ahoj, díky za odpověď.
Tohle by mě nenapadlo.
Samozřejmě mi to stačí takhle, ale zajímalo by mě, jak jsi k tomu došel. Nějak to jde vidět? Něco za tím je? :)
What does a drowning number theorist say?
'log log log log ...'
Offline
#5 28. 03. 2012 21:15
- ruamaixanh

- Místo: Tachov
- Příspěvky: 100
- Reputace: 11
Re: Neizomorfní grupy mající stejný počet prvků všech řádů
Ahoj,
přiznávám, že jsem jenom hledal ve vyhledávači http://answers.yahoo.com/question/index … 955AACoWtr
Offline
#6 28. 03. 2012 21:18 — Editoval Andrejka3 (29. 03. 2012 13:02)
Re: Neizomorfní grupy mající stejný počet prvků všech řádů
↑ ruamaixanh:
Skvělé!
Díky.
edit:
Ověření:
Grupa  je cyklická a každý její prvek. který není jednotkový ji generuje, tedy má řád 3. Odtud, grupa
je cyklická a každý její prvek. který není jednotkový ji generuje, tedy má řád 3. Odtud, grupa 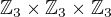 má jeden prvek řádu jedna a 26 prvků řádu 3.
má jeden prvek řádu jedna a 26 prvků řádu 3.
Grupa všech matic 3x3 nad tělesem  s jedničkami na hlavní diagonále, a nulami pod ní:
s jedničkami na hlavní diagonále, a nulami pod ní:
Je třeba ověřit, že řád libovolného nejednotkového prvku této grupy je 3.
volme 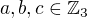 , aspoň jeden různý od nuly a mějme matici:
, aspoň jeden různý od nuly a mějme matici:
1 a b
0 1 c =x, budu značit jen netriviální tři prvky
0 0 1
2a (2b+ac) =x^2 aspon jeden element je nenulový.
2c
3a (3b+3ac) =x^3 = E (jednotkova matice)
3c
PS: museli jsme hledat mezi grupami, jejichž řád není ani p ani p^2, kde p je prvočíslo, aby nebyly automaticky komutativní. Taky je výhodné vzít právě jednu z nich komutativní, protože pak zřejmě nemohou být izomorfní (pokud věříme, že taková dvojice grup existuje). Tak tady je jedna komutativní grupa řádu p^3. Ale nevím, jestli bych k tomuto příkladu nakonec došla.
What does a drowning number theorist say?
'log log log log ...'
Offline
#7 30. 03. 2012 15:48
Re: Neizomorfní grupy mající stejný počet prvků všech řádů
A protože nechci být nepřítelem polopřímého součinu grup, mám tu ještě cvičení navržené kolegou z fóra:
a polopriamy sucin ( semi-direct)
kde
definovany ako
to je příklad podobný předchozímu - dvě neizomorfní grupy se stejným počtem prvků všech řádů.
Když jsem to tu napsala, bude mě to nutit to nakonec dopočítat :)
What does a drowning number theorist say?
'log log log log ...'
Offline
#8 31. 03. 2012 13:07
Re: Neizomorfní grupy mající stejný počet prvků všech řádů
↑ Andrejka3:
Ahoj, len mala poznamka:
Ak chces skutocne najst grupu 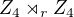 kde
kde 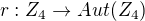 definovany ako
definovany ako 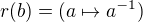
pouzi znamu vetu
V cyklickej grupe,  grupa automorfizmov je isomorfna z grupov inverznych prvkov v okruhu
grupa automorfizmov je isomorfna z grupov inverznych prvkov v okruhu 
( to sa mi zda jedina mozna tazkost na jej vyjadrenie)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 31. 03. 2012 14:50
Re: Neizomorfní grupy mající stejný počet prvků všech řádů
↑ vanok:
Díky za asistenci a rady. Myslím, že k tomuto nebudu další potřebovat, dokud to sama neprojdu. Jen teď potřebuju čas a klid na to si to rozmyslet. Momentálně dělám trochu jiné věci z grup, ale zanedlouho se k tomu vrátím a napíšu, že tomu rozumím a na co jsem přišla.
What does a drowning number theorist say?
'log log log log ...'
Offline
#10 11. 04. 2012 13:26 — Editoval Andrejka3 (11. 04. 2012 13:27)
Re: Neizomorfní grupy mající stejný počet prvků všech řádů
V cyklickej grupe, grupa automorfizmov
je isomorfna z grupov inverznych prvkov v okruhu
No, jestli to je jednodušší cesta, pak ji zatím nepoužiju - neprobrala jsem ještě okruhy.
Někde je chyba, protože když onu grupu, 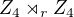 chci najít z definice, chci si nejdřív ověřit některé věci:
chci najít z definice, chci si nejdřív ověřit některé věci:
(1): 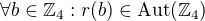 : to je pravda, protože zobrazení
: to je pravda, protože zobrazení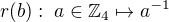 je zřejmě bijektivní. Je to grupový homomorfismus díky komutativitě v
je zřejmě bijektivní. Je to grupový homomorfismus díky komutativitě v 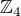 .
.
(2):  je grupový homomorfismus: to není pravda, protože pokud si zvolím libovolné
je grupový homomorfismus: to není pravda, protože pokud si zvolím libovolné 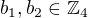 , je na jednu stranu
, je na jednu stranu , kdežto
, kdežto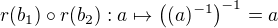 . Protože v
. Protože v 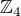 existuje prvek s řádem vyšší než dvě, není vždy
existuje prvek s řádem vyšší než dvě, není vždy 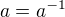 .
.
What does a drowning number theorist say?
'log log log log ...'
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Neizomorfní grupy mající stejný počet prvků všech řádů (TOTO TÉMA JE VYŘEŠENÉ)