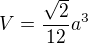Matematické Fórum

FlyingMonkey

Ahoj :)

Prosím o pomoc, nevím si rady:
mám vypočítat objem a povrch čtyřstěnu, když vím, že jeho síť je rovnostranný trojúhelník ...

Nemám zadané nic ... Napadlo mě si ten čtyřstěn v hlavě složit a zkusit dopočítat tu výšku přes nějakou pythagorovku, ale neznám to a, takže nemůžu dopočítat nic konkrétního ...

Díky za rady

teolog · 31. 03. 2012 17:43

↑ FlyingMonkey:
Zdravím,
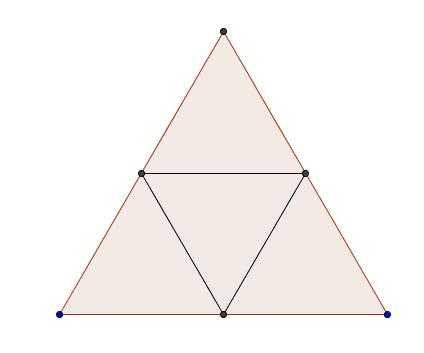
pomůže obrázek sítě?
Uprostřed je podstava a ty okraje jsou stěny.

FlyingMonkey · 31. 03. 2012 18:29

Ahoj,

díky ... Tohle já si představil v hlavě a jde vidět, že výška půjde z těžiště podstavy. bohužel nevím, jak to spočítat tyo ...

Obsah spočítat zvládnu. Jednoduše to bude 4*trojúhelník, kde si získám výšku těch jednotlivých trojúhelníků z pythagorovky...
Ale ten objem nevím ... Díky

teolog · 31. 03. 2012 18:35

↑ FlyingMonkey:
Když to sbalíme a představíme si výšku čtyřstěnu, tak si pak představme pravoúhlý trojúhelník, jehož odvěsny jsou výška čtyřstěnu, třetina výšky v podstavě a výška bočního trojúhelníku).

FlyingMonkey · 31. 03. 2012 22:30

Tak ještě přeci mám problém :)

nekoresponduje mi to s výsledkem ^^

Přes pythagorovku získám výšku jednoho toho trojúhelníku:

$\frac{3}{\sqrt{2}}a$ to je dobře, že?
následně znovu přes pythagorovku, získám h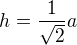
$h=\frac{1}{\sqrt{2}}a$

Potom, už se jenom snažím dosadit do vzorce:

$V=\frac{\sqrt{2}}{12}(\sqrt{2}h)^3 = \frac{4\sqrt{2}h^3}{12}=\frac{\sqrt{2}}{3}h^3$

a to nesedí, kde dělám chybu prosím? Díky!

teolog · 31. 03. 2012 22:57

↑ FlyingMonkey:
Mně ta výška jednoho trojúhelníka vychází $\frac{\sqrt{3}a}{4}$ .

FlyingMonkey · 31. 03. 2012 23:05

To jsem blázen :D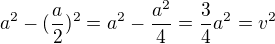

$a^{2}-(\frac{a}{2})^2= a^2 - \frac{a^2}{4}=\frac{3}{4}a^2=v^2$
v= $\frac{\sqrt{3}}{2}a$

jestli už neumím vypočítat ani pythagorovku, tak si jdu hodit asi mašli :D

Díky

teolog · 31. 03. 2012 23:55

↑ FlyingMonkey:
Aha, tak já jsem bral a jako stranu toho velkého trojúhelníka. Pokud je a strana toho menšího pak to je skutečně $\frac{\sqrt{3}}{2}a$ .

FlyingMonkey · 01. 04. 2012 14:59

Dobře tedy, ale pak mi to teda furt nevychází hmm ...

mám teda tu výšku toho jednoho trojúhelníku ... $\frac{\sqrt{3}}{2}a$ , pak počítám přes pythagorovku tu výšku CELÉHO čtyřstěnu

$(\frac{\sqrt{3}}{2}a)^2-(\frac{1}{3}a)^2=h^2$
$h=\frac{\sqrt{23}}{6}a$

$V=\frac{\sqrt{2}}{12}a^3$

$V=\frac{\sqrt{2}}{12}(h\frac{6}{\sqrt{23}})^3=\frac{216\sqrt{2}}{276\sqrt{23}}h^3=\frac{18\sqrt{2}}{23\sqrt{23}}h^3$

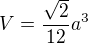
Už fakt nevím, .......................... thx za pomoc

teolog · 01. 04. 2012 17:03 — Editoval teolog (01. 04. 2012 17:05)

↑ FlyingMonkey:
Pozor, ta jedna třetina je třetina výšky, ne strany a.

Mně ta výška čtyřstěnu vychází: $\frac{\sqrt{6}a}{3}$

FlyingMonkey · 02. 04. 2012 19:47

Super, to mi teď taky vychází, ale výsledek je pořád mimo, má to vyjít:

$V = \frac{h^3}{36}\sqrt{\frac{2}{3}}$

Mně vychází stále: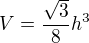

$V = \frac{\sqrt{3}}{8}h^3$

Díky :))

Tychi · 02. 04. 2012 19:59

Proč myslíš, že to tak má vyjít?
$V = \frac{\sqrt{3}}{8}h^3$ odpovídá vzorci pro výpočet objemu pomocí strany $V=\frac{\sqrt2}{12}a^3$

FlyingMonkey · 02. 04. 2012 20:28

Mno máme takhle výsledky ... lámu si tady nad tím hlavu jak ***** :)) ...

Nemůžu objevit, kde bych měl chybu, chmpf ~~

Tychi · 02. 04. 2012 21:11

Už tam chybu nemáš a dál to neřeš(o:

FlyingMonkey · 02. 04. 2012 21:21

Njn, díky .... :) Asi se náš profesor zase překoukl......

To je něco na ty moje nervíčky :D

Johana16 · 08. 04. 2019 08:27

↑ teolog:
Dobrý den, prosím, jak jste přišel na tu jednu třetinu výšky? Děkuji za odpověď

Al1 · 09. 04. 2019 17:54

↑ Johana16:
Zdravím,
výška čtyřstěnu prochází těžištěm podstavy. A těžiště trojúhelníku leží na těžnici 1/3 od strany (a 2/3 od vrcholu) trojúhelníku.

Matematické Fórum

#1 31. 03. 2012 17:00 — Editoval FlyingMonkey (31. 03. 2012 17:01)

Síť pravidelného čtyřstěnu

#2 31. 03. 2012 17:43

Re: Síť pravidelného čtyřstěnu

#3 31. 03. 2012 18:29

Re: Síť pravidelného čtyřstěnu

#4 31. 03. 2012 18:35

Re: Síť pravidelného čtyřstěnu

#5 31. 03. 2012 22:30

Re: Síť pravidelného čtyřstěnu

#6 31. 03. 2012 22:57

Re: Síť pravidelného čtyřstěnu

#7 31. 03. 2012 23:05

Re: Síť pravidelného čtyřstěnu

#8 31. 03. 2012 23:55

Re: Síť pravidelného čtyřstěnu

#9 01. 04. 2012 14:59

Re: Síť pravidelného čtyřstěnu

#10 01. 04. 2012 17:03 — Editoval teolog (01. 04. 2012 17:05)

Re: Síť pravidelného čtyřstěnu

#11 02. 04. 2012 19:47

Re: Síť pravidelného čtyřstěnu

#12 02. 04. 2012 19:59

Re: Síť pravidelného čtyřstěnu

#13 02. 04. 2012 20:28

Re: Síť pravidelného čtyřstěnu

#14 02. 04. 2012 21:11

Re: Síť pravidelného čtyřstěnu

#15 02. 04. 2012 21:21

Re: Síť pravidelného čtyřstěnu

#16 08. 04. 2019 08:27

Re: Síť pravidelného čtyřstěnu

#17 09. 04. 2019 17:54

Re: Síť pravidelného čtyřstěnu

Zápatí