Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Počty malých grup (hrátky s tabulkami) (TOTO TÉMA JE VYŘEŠENÉ)
#1 01. 04. 2012 11:18 — Editoval Andrejka3 (01. 04. 2012 11:28)
Počty malých grup (hrátky s tabulkami)
Dobrý den,
beru to spíše jako oddechové téma.
Grupy řádu 6
Každá grupa řádu 6 je izomorfní jedné z následujících grup: 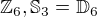 .
.
Dokaž (že žádné další neexistují).
Podle Frobenius-Stickelberger věty jsou všechny komutativní grupy řádu 6 izomorfní grupě 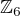 . Chci úplnou indukcí ukázat, že
. Chci úplnou indukcí ukázat, že  je jediná nekomutativní grupa řádu 6. Za tím účelem definuji následující:
je jediná nekomutativní grupa řádu 6. Za tím účelem definuji následující:
Ať 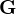 je grupa,
je grupa,  . Definuji posloupnost
. Definuji posloupnost  tak, že
tak, že 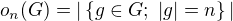 . Díky Lagrange větě,
. Díky Lagrange větě,  . Zřejmě je
. Zřejmě je 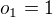 a nekomutativní grupy neobsahují prvek řádu
a nekomutativní grupy neobsahují prvek řádu 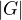 , tedy mě bude zajímat jen podposloupnost
, tedy mě bude zajímat jen podposloupnost 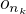 pro zbývající řády prvků, které Lagrange věta nezakazuje.
pro zbývající řády prvků, které Lagrange věta nezakazuje.
Ať tedy 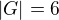 .
.
Pozorování:
Grupa mající jen prvky řádu nejvýše 2 je komutativní. Máme tedy  .
.
Je-li 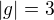 , pak
, pak 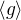 je cyklická a obsahuje ještě jeden inverzní prvek řádu 3,
je cyklická a obsahuje ještě jeden inverzní prvek řádu 3, 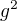 . Odtud, musí být
. Odtud, musí být  sudé.
sudé.
Protože  , připadají v úvahu jen tyto posloupnosti:
, připadají v úvahu jen tyto posloupnosti: 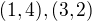 . Posloupnost odpovídající grupě
. Posloupnost odpovídající grupě  je
je  . Chci nyní vyloučit případ
. Chci nyní vyloučit případ 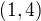 .
.
Předpokládejme, že máme grupu řádu 6, se strukturou 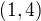 . Chci sestrojit její Cayley tabulku. Označme její prvky řádu dva, resp. 3 jako
. Chci sestrojit její Cayley tabulku. Označme její prvky řádu dva, resp. 3 jako  , resp.
, resp. 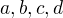 . Ať
. Ať 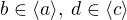 .
.
Protože v každém sloupci i řádku musí být každý prvek grupy právě jednou (levé a pravé translace každé grupy jsou automorfismy grupy), nezbývá, než aby místo otazníku bylo  . Pak ale v políčku pod ním volbou libovolného prvku porušíme vlastnost kvazigrupy a tedy máme spor s tím, že
. Pak ale v políčku pod ním volbou libovolného prvku porušíme vlastnost kvazigrupy a tedy máme spor s tím, že 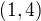 je struktura nějaké nekomutativní grupy.
je struktura nějaké nekomutativní grupy.
Zabývejme se případem  . Označme
. Označme 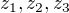 , resp.
, resp. 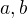 prvky řádu dva, resp. řádu 3.
prvky řádu dva, resp. řádu 3.
Produkty typu 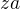 musí být řádu dva. Proto produkty typu
musí být řádu dva. Proto produkty typu  musí být řádu tři (pro
musí být řádu tři (pro 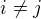 ). BÚNO (volba automorfismu) ať
). BÚNO (volba automorfismu) ať 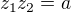 . Další volbu už učinit nemůžeme a vyjde Cayleyho tabulka grupy, která je izomorfní
. Další volbu už učinit nemůžeme a vyjde Cayleyho tabulka grupy, která je izomorfní  .
.
Dokážete, že (až na izomorfismus) neexistují další grupy řádu 8 než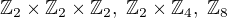 a
a 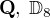 , kde
, kde 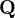 je kvaternionová grupa a
je kvaternionová grupa a  je grupa všech symetrií pravidelného 4-úhelníka?
je grupa všech symetrií pravidelného 4-úhelníka?
Máte nějaké nápady, jak takové problémy řešit?
What does a drowning number theorist say?
'log log log log ...'
Offline
- (téma jako vyřešené označil(a) Andrejka3)
#2 02. 04. 2012 10:45 — Editoval Andrejka3 (02. 04. 2012 22:35)
Re: Počty malých grup (hrátky s tabulkami)
Kdybych měla postupovat stejně jako u grup řádu 6, napsala bych si možnosti, kolik prvků může být jakého řádu. Zajímají mě jen nekomutativní grupy, protože tvrzení o komutativních je zřejmé z Frobenius-Stickelberger věty.
Každá grupa sudého řádu má aspoň jeden prvek řádu dva:  .
.
Abychom nedostali komutativní grupu, musí mít aspoň jeden prvek řádu čtyři:  .
.
Vezmu-li si nějaký takový prvek řádu čtyři,  , pak
, pak 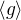 obsahuje ještě jeden prvek řádu čtyři,
obsahuje ještě jeden prvek řádu čtyři,  (značme operaci inverze čárkou), a jeden prvek řádu dva:
(značme operaci inverze čárkou), a jeden prvek řádu dva: 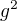 . Odtud je jasné, že
. Odtud je jasné, že 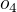 je sudé číslo. Možné struktury - posloupnosti
je sudé číslo. Možné struktury - posloupnosti 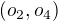 pro nekomutativní grupy řádu 8 jsem zredukovala na:
pro nekomutativní grupy řádu 8 jsem zredukovala na: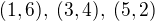 . Jde vidět, že v případě
. Jde vidět, že v případě 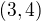 , si ještě mohu vybrat, kolik různých prvků druhého řádu lze napsat jako "druhá mocnina nějakého prvku (čtvrtého řádu)". Takové věci se dají očekávat, protože může existovat více neizomorfních grup se stejnou posloupností viz mé předchozí téma.
, si ještě mohu vybrat, kolik různých prvků druhého řádu lze napsat jako "druhá mocnina nějakého prvku (čtvrtého řádu)". Takové věci se dají očekávat, protože může existovat více neizomorfních grup se stejnou posloupností viz mé předchozí téma.
Porovnáním se strukturou nekomutativních grup 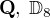 zjistím, která posloupnost je tam navíc. Pojďme nejdříve na případ
zjistím, která posloupnost je tam navíc. Pojďme nejdříve na případ 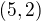
Případ první 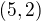
Případ druhý
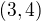
edit:oprava
What does a drowning number theorist say?
'log log log log ...'
Offline
#3 02. 04. 2012 22:45 — Editoval Andrejka3 (03. 04. 2012 00:14)
Re: Počty malých grup (hrátky s tabulkami)
Pokračování druhého případu 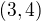
Případ třetí
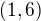
Úplnou indukcí jsem dokázala, že už neexistují (až na izomorfismy) další grupy řádu 8.
edit: Téma je označeno jako vyřešené, ale ráda uvidím nějaké návrhy na zlepšení, jiné cesty, otázky atd
What does a drowning number theorist say?
'log log log log ...'
Offline
#4 03. 04. 2012 09:55
Re: Počty malých grup (hrátky s tabulkami)
U grupy řádu 8 jsem v "Případu druhém" první možnosti narazila na toto:
Dvě podgrupy řádu 3, které mají triviální průnik. Vytvoří tím v tabulce dva bloky (2x2). V pravo vedle horního čtverečku musíme nacpat "řád těch podgrup - 1" dalších prvků. Takže musíme mít k dispozici tady 2 ještě další. Máme ale jen jeden:  . Proto porušíme kvazigrupovitost :) To si uvědomím až budu konstruovat větší grupy, třeba řádu 12 ;)
. Proto porušíme kvazigrupovitost :) To si uvědomím až budu konstruovat větší grupy, třeba řádu 12 ;)
Každopádně kategorizace konečných nekomutativních grup již byla provedena, že?
What does a drowning number theorist say?
'log log log log ...'
Offline
#5 03. 04. 2012 11:07
Re: Počty malých grup (hrátky s tabulkami)
↑ Andrejka3:
Odpoved, co sa tyka jednoduchych grup je aj tu
http://cs.wikipedia.org/wiki/Klasifikac … %BDch_grup
alebo
http://en.wikipedia.org/wiki/Classifica … ple_groups
Co sa tyka teorem uzitocnych na vysetrovanie (malych) konecnych grup, slubujem, ze tu napisem maly zoznam takych teorem.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Počty malých grup (hrátky s tabulkami) (TOTO TÉMA JE VYŘEŠENÉ)
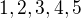 , resp.
, resp. 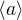 je komutativní, protože její řád je druhá mocnina prvočísla (2^2).
je komutativní, protože její řád je druhá mocnina prvočísla (2^2).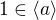
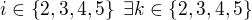 takové, že
takové, že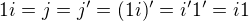 . Tedy
. Tedy  komutuje s každým prvkem.
komutuje s každým prvkem.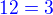 Tím dostaneme komutativní (má prvky řádu nejvýše 2)
Tím dostaneme komutativní (má prvky řádu nejvýše 2) 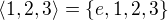 . Doplním do tabulky modrou barvou.
. Doplním do tabulky modrou barvou. analogicky pak
analogicky pak  komutativní podgrupa. Doplním zelenou.
komutativní podgrupa. Doplním zelenou.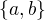 , namísto žlutých otazníku musím doplnit
, namísto žlutých otazníku musím doplnit  .
.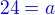 .
.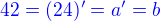 .
.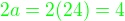 .
. 
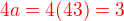 ,
,  .
.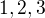 , resp.
, resp. 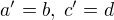
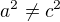 nebo
nebo 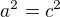 .
. a
a 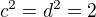 . Podgrupy
. Podgrupy  jsou komutativní. Máme tabulku:
jsou komutativní. Máme tabulku: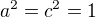 zvolili jsme tento prvek, aby byl společným prvkem druhého řádu v grupách
zvolili jsme tento prvek, aby byl společným prvkem druhého řádu v grupách 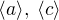
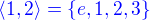 a je komutativní (za prvé to vidíme a za druhé má prvky řádu nejvýše 2).
a je komutativní (za prvé to vidíme a za druhé má prvky řádu nejvýše 2).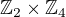 , která má právě takovou strukturu, chci si ušetřit práci zkoumáním komutativity některých prvků grupy. Třeba, komutují mezi sebou prvky grup
, která má právě takovou strukturu, chci si ušetřit práci zkoumáním komutativity některých prvků grupy. Třeba, komutují mezi sebou prvky grup 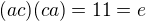
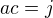 (nejaky prvek druheho radu) a
(nejaky prvek druheho radu) a 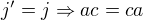 .
.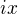 , kde
, kde  je prvek řádu dvě a
je prvek řádu dvě a  prvek řádu 4? Tedy zbývající dva obdélníčky tabulky.
prvek řádu 4? Tedy zbývající dva obdélníčky tabulky.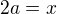

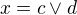
 .
.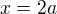
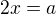


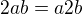
 Odkud plyne komutativita zbytku tabulky. Tato struktura vede na grupu izomorfní
Odkud plyne komutativita zbytku tabulky. Tato struktura vede na grupu izomorfní 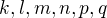
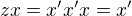
 . Abych se nemotala s
. Abych se nemotala s 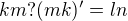 Je místo otazníku rovnítko?
Je místo otazníku rovnítko?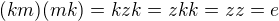 takže ano, zbytek tabulky je antikomutativní.
takže ano, zbytek tabulky je antikomutativní.