Matematické Fórum

↑ check_drummer:
Ahoj, podle zadané definice sledu není 15,16,17,18,19,20 sled, protože obsahuje prvočíslo.
Sled má být složen jen ze složených čísel, jestli jsem to dobře pochopila.
Odtud asi taky plyne, že musí sled n čísel začínat od čísla většího než n.

Co třeba 2,3,4,5? Obsahuje tři prvočísla. Ale teď nevím, zda chceš navíc, aby se začalo aspoň od pětky, když vybírám čtyři čísla.
V tom důkazu jsem si jistá třemi prvočísly, to čtvrté tam nevidím.

↑ Andrejka3:
Já jsem to prvočíslo nijak neoznačil - takže opravdu není vidět, jak píšeš.

↑ Andrejka3:
Ono je to pozorování, když v definici dovolíme jen složená čísla. Já jsem si tam (špatně) "přidal" i prvočísla a proto jsem to bral jako součást definice.
V tom případě ale zbývá najít důkaz pro obecné n - nebo tvrzení vyvrátit. Rovněž tak by bylo hezké v mém důkaze odstranit spoléhání na relativně netriviální tvrzení o rozdílu mocnin čísel 2 a 3.

↑ Andrejka3:
To není žádná věda - když řešíš (jak to tak sleduju) netriviální algebru, tak tohle bys zvládla taky. :-)
Také jsem zvědav jak to dopadne - pro sledy o malých číslech je šance, že budou obsahovat málo prvočísel (z omezeného rozsahu), ale zase jsou zde prvočísla víc hustě rozmístěna. Pro sledy o velkých číslech je to přesně naopak.

Zajímavý už by byl jen fakt jaká je četnost sledů délky n, které obsahují aspoň jedno prvočíslo. Ale asi by bylo možné dát nějaký odhad z prvočíselné věty - i když dost hrubý - tady už vstupuje do hry podmíněná pravděpodobnost.

Sled 5 čísel, který začíná lichým číslem, má v rozkladu alespoň 5 prvočísel.

Mějme sled {a1, a2, a3, a4, a5}, kde a1 je liché, a rozdělme si ho na dva sledy délky 4:
{a1, a2, a3, a4}  a  {a2, a3, a4, a5}

První sled dělí jistě 4 různá prvočísla: g, h, i, j
Druhý sled dělí: k, l, m, n

Alespoň jedno provočíslo dělí a1, můžeme vybrat třeba g. Stejně tak k dělí a5.
Musíme počítat s nejhorším a předpokládat, že h=l a i=m a j=n. Ovšem g != k, protože a1 a a5 jsou nesoudělná. Tedy máme 5 různých prvočísel g, h, i, j, k, což jsme chtěli dokázat.

Ovšem u sledu s prvním sudým číslem je nsd(a1, a5)|4, a tak nelze postup použít, alespoň ne v této podobě.

Ještě jsem se snažil dokázat větu, že žádná 2 čísla sledu nemají stejný "čtvercuprostý" rozklad na prvočísla (neuvažujeme mocniny prvočísel, třeba 6=2*3, 18=2*3, 12=2*3), která by snad mohla být užitečná. Nedostal jsme se ale dál, než že taková 2 čísla by ve svém rozkladu musela mít alespoň 2 prvočísla (protože jedno nemůže být násobkem druhého) a tudíž by jejich rozdíl musel být >= 2*3.

Je z mé hlavy. V jedné bakalářské práci jsem narazil na hypotézu, že existuje prvočíslo mezi n^2 a (n+1)^2 a napadlo mě, že pokud by se podařilo dokázat, že nejmenší číslo ze sledů délky 2n je větší než n^2+1, potom ta hypotéza platí. Včera jsem našel na anglické wiki článek "Prime gap", ve kterém se píše asi o tom samém, ještě jsem to ale nezkoumal.

No, platí-li domněnka, potom , kde 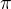udává počet prvočísel menších nebo rovných argumentu a vrací nejmenší číslo ze sledů dané délky, a to je o něco lepší dolní odhad, než že .

↑ check_drummer:
Ano, pro libovolné n. Ale asi ji, pokud tedy je pravdivá, bude těžké dokázat.

I sled 5 čísel, který začíná sudým číslem, má v rozkladu alespoň 5 prvočísel.