Matematické Fórum

FliegenderZirkus

Ahoj,

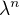jak známo (spectral mapping theorem), tak pokud $\lambda$ je vlastní číslo nějakého tenzoru druhého řádu (nebo v tuhle chvíli stačí reálné čtvercové matice) $\textbf{A}$ , tak $\lambda^n$ je vlastní číslo tezoru 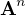$\textbf{A}^n$ . Obecněji to platí pro polynomy, tj. polynom 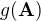$g(\textbf{A})$ má vlastní číslo 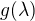$g(\lambda)$ (g je jednou funkcí tenzoru a podruhé funkcí reálného čísla, ale má v obou případech stejné koeficienty).

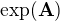Čtu si zrovna důkaz, že $\text{det}[\text{exp}(\textbf{A})]=\text{exp}[\text{tr}(\textbf{A})]$ a tam se bez zdůvodnění používá, že $\text{exp}(\textbf{A})$ má vlastní číslo 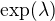$\text{exp}(\lambda)$ , přitom exponenciálna zjevně není polynom. Jde ten spectral mapping theorem skutečně tak jednoduše zobecnit na jakoukoli funkci? Nabízí se nějak argumentovat Taylorovým rozvojem, ale až tak jednoduché to přeci nebude, ne? Jsou funkce, u kterých je s Taylorem trochu problém. Platí to tedy jen pro funkce které jsou všude rovny svým Taylorovým řadám?

Když o tom tak přemýšlím, tak jsme si pro tenzory definovali pouze polynomy, z ostatních funkcí jsme zatím používali jen exponenciálu pomocí definice 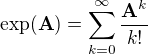$\text{exp}(\textbf{A})=\sum_{k=0}^{\infty}\frac{\textbf{A}^k}{k!}$ . V tuhle chvíli tedy ani nevím, jestli lze ty potencionálně problematické funkce pořádně definovat...

EDIT: Teď to vidím tak, že tenzorové funkce umím (alespoň zatím) definovat jen pomocí mocninných řad, proto pro každou takovou funkci bude platit, že 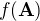$f(\textbf{A})$ má vlastní číslo 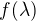$f(\lambda)$ . Je to tak?

Matematické Fórum

#1 15. 04. 2012 22:39 — Editoval FliegenderZirkus (15. 04. 2012 22:42)

Vlastní čísla exponenciály tenzoru (matice)

Zápatí