Matematické Fórum

marram · 22. 04. 2012 17:00

Zdravím, potřebovala bych trochu poradit jak na tyhle typy příkladů:
Např.: 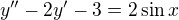$y''-2y' - 3 = 2\sin x$
1) vyřeším rovnici a zjistím kořeny (to zvládám) :D
2) nalézt partikulární řešení, a to děláme pomocí vzorečku
$y_{p}=x^{k} \cdot e^{\alpha x} [Q_{n}(x)\cdot \cos \beta x+ R_{n}(x)\cdot sin\beta x]$

Pak si musím dle zadání najít $\alpha , \beta , Q_{n}(x) a R_{n} (x)$ .

Podle čeho prosím zjistím 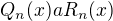$Q_{n}(x) a R_{n}(x)$

Někdy je to A a B, někdy ve tvaru 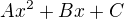$A x^{2}+Bx+C$ apod.

A ať hledám jak hledám na internetu, nemůžu najít odpověď, která by mi pomohla, tak doufám, že mi někdo pomůže tady.
Děkuju moc

mal84 · 22. 04. 2012 17:09

Zdravím.
Polynomy Q(x) a R(x) mají stejný stupeň, jako polynomy vyskytující se na pravé straně rovnice v zadání.
V tomto případě je tam jen výraz 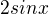$2sinx$ , u sinu je tedy mnohočlen $2$ , to je konstantní mnohočlen, tzn. že polynomy Q a R budou taky konstantní, ve výpočtu se tak bude pracovat s koeficienty A a B.

marram · 22. 04. 2012 17:10

↑ mal84:
Oukej, děkuju moc

mal84 · 22. 04. 2012 17:11

↑ marram:

Respektive ten stupeň bude roven většímu ze stupňů polynomů v zadání..

Matematické Fórum

#1 22. 04. 2012 17:00

Diferenciální rce n-tého řádu

#2 22. 04. 2012 17:09

Re: Diferenciální rce n-tého řádu

#3 22. 04. 2012 17:10

Re: Diferenciální rce n-tého řádu

#4 22. 04. 2012 17:11

Re: Diferenciální rce n-tého řádu

Zápatí