![$\lim_{\to\infty }\frac{\sqrt{x+\sqrt{x}}-1}{\sqrt[3]{x}-\sqrt{x}}$](/mathtex/9f/9fb116cb9ecef8eb8c77ab1f9e7e61b0.gif "kopírovat do textarea")
![$\sqrt[3]{x}$](/mathtex/53/537f3e3eae88063acab693151571f957.gif "kopírovat do textarea")
#4 01. 05. 2012 23:55 — Editoval kaja.marik (01. 05. 2012 23:57)
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Limita
nejvyssi mocnina ve jmenovateli je odmocnina z x
btw: dokazala byste vysvetlit Vase navrhy?
Offline
?#7 10. 05. 2012 14:22
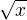![$\frac{\sqrt{x+\sqrt{x}}-1}{\sqrt[3]{x}-\sqrt{x}}=\frac{\frac{\sqrt{x+\sqrt{x}}}{\sqrt{x}}-\frac{1}{\sqrt{x}}}{\frac{\sqrt[3]{x}}{\sqrt{x}}-1}$](/mathtex/cf/cf0fb70d76b0a4fb5336c3bc404d650c.gif "kopírovat do textarea")
Offline