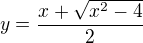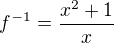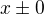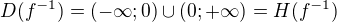Matematické Fórum

leniczcha · 03. 05. 2012 11:07

y = (x + odmocnina (x^2 - 4)) / 2 x >=2

vyšlo mi:

f-1 (x) = (x^2 + 1) / x

Jediné v čem je problém, že D(f-1) by měl být <1,+nekonečno) a to nevím proč.

rleg · 03. 05. 2012 11:23 — Editoval rleg (03. 05. 2012 11:56)

↑ leniczcha: Ahoj
Je to proto, že $H(f)=<1;+\infty) \Rightarrow D(f^{-1})=<1;+\infty)$

EDIT:
Jsem se na to teď podívalpořádně a vyšlo mi, že
$D(f)=(-\infty ;-2> \cup <2;+\infty ) \nl H(f)=<-1;0)\cup <1;+\infty )$

leniczcha · 03. 05. 2012 11:28

↑ rleg:
Proč nemohu prostě určit z předpisu inverzní funkce definiční obor? V tomto případě by se x nemělo rovnat nule.

leniczcha

$y=\frac{x+\sqrt{x^{2}-4}}{2}$

Po úpravách vyšlo:
$x=\frac{y^{2}+1}{y}$

Tedy inverzní funkce:
$f^{-1}=\frac{x^{2}+1}{x}$

Z inverzní funkce si určím definiční obor:
$x\pm 0$

$D(f^{-1})=(-\infty ;0)\cup (0;+\infty )=H(f^{-1})$

Ve výsledcích je:

$D(f^{-1})=<1;+\infty )$

Poradí někdo, jak by to mělo být?

rleg · 04. 05. 2012 08:14

Zhruba takto: Abys mohla vytvořit fci inverzní, tak původní fce musí být prostá a pokud je spojitá, tak i monotonní. Fce původní a inverzní jsou souměrné podle přímky y=x

Pro fci původní a inverzní platí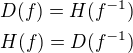
$D(f)=H(f^{-1}) \nl H(f)=D(f^{-1})$

Protože je původní fce prostá, proto bude i fce inverzní prostá a ta inverzní fce, kterou jsi našla je prostá právě v intervalu $D(f^{-1})=<-1;0)\cup <1;+\infty )$

Nevím, proč máš ve výsledcích uvedený pouze část $D(f^{-1})$ , podle mě by tam mohl být celý, souměrné to je.

Názorně to je vidět třeba na fci sin a arcsin. Jelikož fce sin sama o sobě není prostá, vybereme k řešení pouze interval ve kterém prostá je. To je důvod proč fce arcsin má $D(f)=<-\frac{\pi}{2};+\frac{\pi}{2}>$

Matematické Fórum

#1 03. 05. 2012 11:07

Inverzní funkce

#2 03. 05. 2012 11:23 — Editoval rleg (03. 05. 2012 11:56)

Re: Inverzní funkce

#3 03. 05. 2012 11:28

Re: Inverzní funkce

#4 03. 05. 2012 18:23 — Editoval leniczcha (03. 05. 2012 18:24)

Re: Inverzní funkce

#5 04. 05. 2012 08:14

Re: Inverzní funkce

Zápatí