Matematické Fórum

Nemá někdo zadání ať můžeme diskutovat?

↑ dawemaslo:
To bylo 72.

Nazdar,
tak první číslo bylo 72, mělo ho u nás 5 z 6 lidí :)
Dále jsem snad vyřešil ty logaritmy:
zadání



a)urči V(3)
b)urči V(5)/V(4)
c)urči V(100)-V(99)

výsledky jsem napsal a) 2log2 b) 3/2 c) 0

u první dvou jsem to jenom spočítal. u třetího nevím, zda mi uznají postup

Myslíte si, že u sestrojení té kružnice, ze které jde vidět úsečka pod úhlem 30°, musí být i postup konstrukce?
Byla to tuším 12.

Nechcete sem kdyžtak dávat i počet bodů? Já abych si spočítala, jestli to dám... :)
Díky!

↑ VitasKreuz:
snad ne, tam nikde není napsáno, že musí ne? Já tam teda mám jen vytáhnutej ten oblouk propiskou

dalsi priklad)

usecka AB, .

usecka je videt z bodu X pod uhlem .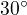

1) sestrojte mnozinu vsech bodu, ze kterych je usecka AB videt pod stejnym uhlem.
2) urcit bod Y v mnozine z 1), ktery je od bodu B nejdal
3) urcit tuto vzdalenost

reseni: stredove/obvodove uhly. do archu chteli i konstrukci. takze stredovy uhel , sestrojit pomoci kruzitka.

+ kdyz jde o 60 stupnu, tak "pomocny trojuhelnik" je rovnostranny => |AB|=r
nejvzalenejsi bod by mel byt na spojnici bodu B, se stredem S a to ve vzdalenosti 2r=700 asi. cisla si presne nepamatuji

Dál si pamamtuju, že tam byla otázka s tou elipsou, otázka vzdělaní//bohatí, a ta kružnice která měla tak trochu ošemetné zadání...

Jinak ot.č. 6 myslím (určit kvocient?) mi vyšel 16

↑ ceresi:

otazka 6 bylo zjistit kvocient z pomeru dvou clenu geom. posloupnosti a z toho urcit pomer dalsich dvou. z prvniho pomeru vyslo q^2 = 4, a ten pomer dalsich clenu byl q^4, takze 16.

Pamatujete si někdo zadání toho kvocientu s geometrcikou posloupností. Mě to teda vyšlo 2

Ta elipsa vyšla 3, bylo to vlastně a (hlavní poloosa)

23)

Platí

Rozhodni (ano/ne)
1. Jeden z koeficientu (b,c,d) je 0
2. Právě jeden koeficient je záporný
3.