Matematické Fórum

Saturday · 05. 11. 2008 21:25

Právě bádám nad takovou drobností:

Ve skriptech prof. Štěpánka na straně 32 - Lemma 2.33 (de Morganova pravidla) se v důkazu objevilo, že díky tomu, že platí:

$\vdash \neg \neg A \leftrightarrow A$ (1)

tak použitím věty o ekvivalenci (ve skriptech asi o dvě strany zpět) platí:

$\vdash \neg \neg (A \rightarrow \neg B) \leftrightarrow (A \rightarrow \neg B)$ (2)

Intuitivně je mi to jasné, ale není mi jasné, jak je to formálně přesně napasováno na větu o ekvivalenci.

Chceme nahradit A (tj. podformule (1), označme tuto podformuli 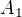$A_1$ ) formulí $(A \rightarrow \neg B)$ (tj. podformule (2), označme tuto podformuli $A_1'$ ), což ale nesplňuje požadavek věty o ekvivalenci:

$\vdash A_1 \leftrightarrow A_1'$

Jaká je tedy správná cesta?

==============================
skripta v postscriptu: http://kti.mff.cuni.cz/downloads/Pl_ps.zip
skripta v DVI formatu: http://kti.mff.cuni.cz/downloads/Pl_dvi.zip

Díky za pomoc!

Matematické Fórum

#1 05. 11. 2008 21:25

Výroková logika - věta o ekvivalenci

Zápatí