Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 05. 2012 10:16
- elijah
- Příspěvky: 151
Rešení kvadratické rovnice
Dobrý den, řeším rovnici 
nevím jak se dostat na výsledný tvar:
Podle mě by se to mělo řešit takto:


Kde je chyba ?
Offline
- (téma jako vyřešené označil(a) elijah)
#3 19. 05. 2012 13:24 — Editoval elijah (19. 05. 2012 13:26)
- elijah
- Příspěvky: 151
Re: Rešení kvadratické rovnice
↑ marnes:
No jde mi spíš o tu upravu, jelikož jsem vycházel z tudma kde je zadaný ten příklad jak jsem psal výše
a výsledek po úpravách je označený jako
Teprve pak by se měl dělat diskriminant adt, ale nechápu jak se k tomu dospělo, a není to tam uvedeno.
Ja bych došel k tomuto:
Proto se ptám, kde je chyba ?
Offline
#5 19. 05. 2012 15:57
- elijah
- Příspěvky: 151
Re: Rešení kvadratické rovnice
↑ zdenek1:
Ahaaa, tak to jsem špatně pochopil. Tak v tom případě děkuji. A ten můj postup by tedy byl správně ? u toho příkladu ?
Offline
#7 19. 05. 2012 17:56 — Editoval elijah (19. 05. 2012 17:56)
- elijah
- Příspěvky: 151
Re: Rešení kvadratické rovnice
↑ zdenek1:
A mužu vědět proč bych se nemohl zbavit te odmocniny ? nevim jak bych počítal s tou odmocninou ze dvou jelikož 1-sqrt(2) =-0.41421 což mi moc eleganstní pro výpočet nepřijde.
Offline
#8 19. 05. 2012 21:00
Re: Rešení kvadratické rovnice
↑ elijah:
Když umocňuješ, tak násobíš výraz jím samým, takže  tě odmocniny nezbaví.
tě odmocniny nezbaví.
ad elegance: tak to nech ne tvaru  - výsledek výjde vcelku pěkný -
- výsledek výjde vcelku pěkný -  - pokud se nepletu
- pokud se nepletu
Radim, tedy jsem.
Dobrá rada je drahá, ta moje je zdarma.
Offline
#10 20. 05. 2012 00:01
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rešení kvadratické rovnice
↑ jarrro:
:-) Založ si téma s anketou a nezapomeň na variantu "V Lážově je krásně za každého počasí".
--------------------------------------------
ano, souhlasím s kolegou rleg, co do výsledku.
Lze považovat za vyřešené? Děkuji.
Offline
#11 20. 05. 2012 07:10
- elijah
- Příspěvky: 151
Re: Rešení kvadratické rovnice
↑ jelena:↑ rleg:
Díky, ten váš postup sem pochopil, ale co nechápu je, že když teda násobím výraz tím samým:
Tak mi stejně vyjde x^4 Viz Wolfram
A s tím umocnováním jste mě teda dostali, vždycky jsem měl za to, že se té odmocniny dá zbavit a je to tak i v několika příkladech, že se na jedné straně odstraní a zbytek se umocní na druhou. Viz:

A dokonce i jeden příklad tady na Foru ten samý postup.
Takže teď jsem z toho zmatený, nevim jestli to platí jen někdy nebo jak se to naučit abych si pak byl jistý, protože jestli se každý příklad řeší jinak tak to se tu matiku asi nikdy nenaučím.
Offline
#13 20. 05. 2012 10:23
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rešení kvadratické rovnice
↑ gogy27:
děkuji, ještě pro kolegu dolním:
při řešení rovnice lze uvažovat úpravy povolené a nepovolené. Nepovolená úprava je chybné použití vzorce  , které máš v prvním příspěvku a další úpravy, co povedou na úplnou změnu zadání.
, které máš v prvním příspěvku a další úpravy, co povedou na úplnou změnu zadání.
V povolených úpravách už uvažujeme úpravy ekvivalentní (nevyžaduji určení podmínek úprav) a neekvivalentní (třeba stanovit podmínku úpravy, jak doporučuje ↑ gogy27:.
Ty v úvodním zadání máš kvadratickou rovnici, která se má řešit jedním z vhodných postupů pro řešení kvadratických rovnic. Tak se nedostaneš do slepých ulic. Řešení matematických úloh se skládá ze standardních postupů, každý příklad se neřeší "jinak", ale volbou vhodného a správného postupu. Procvičením se dostáváš do rutiny, co se tyče volby a použití postupů.
Ať se vede.
Offline


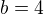

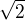 ? podobne 3.141592 miesto
? podobne 3.141592 miesto 
 sa dá umocniť ale nesmieme zabudnúť na podmienky, že
sa dá umocniť ale nesmieme zabudnúť na podmienky, že 

