Matematické Fórum

Kony · 21. 05. 2012 19:08

Dobrý den,

zkoušel jsem se dívat zde po různých tématech ale nenašel jsem zde nic co by mi pomohlo vypočítat tuto úlohu. Byl bych velmi rád kdyby se mi aspoň někdo pokusil vysvětlit postup jak daný příklad vypočítat.

Děkuji moc za případnou pomoc.

Rozhodněte, zda zobrazení $\varphi : \mathbb{R}^{3} \Rightarrow \mathbb{R}^{2}$ definované předpisem $\forall (x,y,z) \in \mathbb{R}^{3}$ : $\varphi ((x,y,z)) = (x,y+z)$ je lineární. Pokud ano, určete jádro a obraz tohoto zobrazení.

vosa · 21. 05. 2012 21:19

Ahoj,
Nejprve máš ověřit linearitu zobrazení. To znamená, že máš ověřit zda pro tvoje zobrazení platí:
$(\forall a \in \mathbb{R}^3)(\forall b \in \mathbb{R}^3)(\varphi(a+b) = \varphi(a) + \varphi(b))$
$(\forall a \in \mathbb{R}^3)(\forall \alpha \in \mathbb{R})(\varphi(\alpha a) = \alpha \varphi(a))$

Až zjistíš, že je zobrazení lineární, budeš hledat jeho jádro, to znamená takový vektor (x, y, z), pro který platí, že $\varphi(x,y,z) = (0,0)$ to znamená $(x, y+z) = (0,0)$ to vede na soustavu dvou lineárních rovnic, kterou snadno vyřešíš.

Nakonec budeš hledat obraz. To lze udělat tak, že vezmeš nějakou bázi prostoru 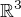$\mathbb{R}^3$ , najdeš obrazy jejích vektorů a z těchto obrazů pak vybereš lineárně nezávislý soubor vektorů - to bude báze obrazu.

Je to vše jasné?

Kony · 21. 05. 2012 21:50

↑ vosa:

Dobrý večer,

díky tvému vysvětlení a mých skript jsem pochopil jak vyhledat jádro ale vyhledání obrazu mi stále uniká. Byla bys tak hodná a napsala bys mi postup jak ten obraz vyhledat???

Díky moc.

vosa · 21. 05. 2012 21:57

Tak vezmu si například standardní bázi prostoru R^3, která má vektory:
$e_1 = (1,0,0), e_2 = (0,1,0), e_3 = (0,0,1)$
Postupně najdu jejich obrazy:
$\varphi(e_1) = (1,0), \varphi(e_2) = (0,1), \varphi(e_3) = (0,1)$
Soubor těchto tří vektorů generuje obraz, ze souboru vyberu lineárně nezávislé vektory, ty budou tvořit bázi obrazu. Je zřejmé, že to jsou vektory (1,0) a (0,1), obraz je tedy jejich lineárním obalem.

Linearita toho zobrazení se ti povedla ověřit?

Kony · 21. 05. 2012 22:23 — Editoval Kony (22. 05. 2012 20:39)

↑ vosa:

Myslím, že ano. Postupoval jsem takto:

f (x1, y1, z1) + f ( x2, y2, z2) = (x1, y1 + z1) + (x2, y2 + z2) =

=(x1 + x2, y1 + z1 + y2 + z2)=

=f (x1 + x2, y1 + y2, z1 + z2)=

=f (x1,y1,z1) + (x2,y2,z2).

A podobně jsem to dokázal pro druhoi vlastnost.

vosa · 21. 05. 2012 22:33

fajn

Kony · 21. 05. 2012 22:38

↑ vosa:

Díky za vysvětlení :)

Matematické Fórum

#1 21. 05. 2012 19:08

Určení zobrazení, jeho jádra a obraz

#2 21. 05. 2012 21:19

Re: Určení zobrazení, jeho jádra a obraz

#3 21. 05. 2012 21:50

Re: Určení zobrazení, jeho jádra a obraz

#4 21. 05. 2012 21:57

Re: Určení zobrazení, jeho jádra a obraz

#5 21. 05. 2012 22:23 — Editoval Kony (22. 05. 2012 20:39)

Re: Určení zobrazení, jeho jádra a obraz

#6 21. 05. 2012 22:33

Re: Určení zobrazení, jeho jádra a obraz

#7 21. 05. 2012 22:38

Re: Určení zobrazení, jeho jádra a obraz

Zápatí