Matematické Fórum

Aquabellla · 26. 05. 2012 18:27

Zdravím, procházím různé příklady a tenhle nevím, jak vyřešit. Vždy jsme řešili jen rotaci, ale symetrii vůbec. Předem děkuji za každou radu.

Lineární operátor 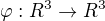$\varphi: R^3 \rightarrow R^3$ je symetrií podle přímky 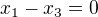$x_3 - x_2 = 0$ , $x_1 - x_3 = 0$ . Najděte matici A ve standardních souřadnicích tak, aby platilo 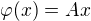$\varphi(x) = Ax$ . Řešení doprovoďte slovním komentářem.

LukasM · 27. 05. 2012 10:08 — Editoval LukasM (27. 05. 2012 10:09)

↑ Aquabellla:
Zkusil bych tohle. Vzal bych vektor té přímky a dva k němu kolmé vektory tak, abych měl 3 LN vektory. Pak bych měl být schopen říct, kam se tyto vektory zobrazí (co udělá osová souměrnost s takovými vektory?) Tím budeme mít obrazy 3 LN vektorů, a tedy zobrazení je kompletně popsáno a můžeme sestavit jeho matici v libovolných bázích.

Aquabellla · 27. 05. 2012 12:09

↑ LukasM:

Směrový vektor přímky je 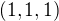$(1, 1, 1)$ . Dva kolmé vektory můžu vzít normálové vektory přímky 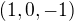$(0, -1, 1)$ , $(1, 0, -1)$ a zortogonalizovat, aby byly na sebe navzájem kolmé.

Vektory jsou: 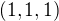$(1, 1, 1)$ , $(0, -1, 1)$ a $(1, -\frac12, -\frac12)$ .

Osová souměrnost zachová jejich kolmost. Víc mě nenapadá.

LukasM · 27. 05. 2012 12:55

↑ Aquabellla:
Ortogonalizovat bych řekl není nutné. Určitě to neublíží, ale je to podle mně zbytečné.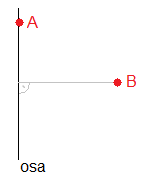

Na co se zobrazí bod A? Na co bod B?

Upozorňuju, že jsem to nepočítal, a nevím jestli to vede ke správnému řešení.

vanok · 27. 05. 2012 13:10

↑ Aquabellla:
Pozdravujem.
Mala poznamka: kolma (Cize ortogonalna symetria) k danej priamke nie je nic ine ako rotacia uhla miery $\pi$ okolo danej priamky.

Aquabellla

↑ LukasM:

Bod A se zobrazí sám na sebe. Bod B se zobrazí na svůj obraz B'.
Jelikož B leží na přímce, která je kolmá k ose, bude i B' ležet na stejné přímce, jen vektor bude mínus násobek.

↑ vanok:
Děkuji, to mě nenapadlo.

(1 0 0 ) (1 0 0)
(0 cos(pi) sin(pi) ) = (0 -1 0)
(0 sin (pi) -cos(pi)) (0 0 1)

vanok · 27. 05. 2012 16:54

↑ Aquabellla:,
Ano, ale upresni v akej baze je napisana tvoja matica.
Vseobecne na urcenie "vektorovych" aplikacii staci urcit obraz jednej bazy.

Aquabellla · 27. 05. 2012 17:16

↑ vanok:

Řekla bych, že to bude v bázi $\alpha$ , což je báze, která obsahuje ty tři navzájem kolmé vektory. Takže abych získala matici v kanonické bázi, stačí udělat součin:
$A = (\varphi)_{\epsilon, \epsilon} = (id)_{\epsilon, \alpha} \cdot (\varphi)_{\alpha, \alpha} \cdot (id)_{\alpha, \epsilon}$
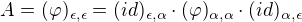
Je to tak?

LukasM · 27. 05. 2012 18:02

↑ Aquabellla:
Je to jedna z možností. Jinak se mi zdá, že v té matici rotace máš chybu. Ta matice by podle mého měla mít na diagonále dva mínusy, ne jen jeden.
Dá se spekulovat o tom, jestli není zbytečné to zavádění rotace, i když je jistě správně. Jakmile totiž vím, že má platit A(1,1,1)=(1,1,1), A(0,-1,1)=(0,1,-1) a A(-1,0,1)=(1,0,-1), můžu okamžitě napsat matici zobrazení v bázích E,X, a zbytek je jen převedení do std báze (X značím bázi tvořenou těmi třemi vektory). Pak by to mělo jít udělat bez znalosti matice rotace a jen s jedním převodem mezi bázemi.

Aquabellla · 27. 05. 2012 18:43

↑ LukasM:

Díky moc za vysvětlení, teď už tomu rozumím.

vanok · 27. 05. 2012 19:20 — Editoval vanok (27. 05. 2012 19:21)

↑ Aquabellla:
poznamka
tvoja "rotacia" ma maticu
(1 0 0 ) (1 0 0)
(0 cos(pi) -sin(pi) ) = (0 -1 0)
(0 sin (pi) cos(pi)) (0 0 -1)

Ale akej baze?: V takej baze B, ze su v nej vyjadrene vektory ako ajich obrazy
prvy jednodkovy vektor je na "osy" aplikacie ( cize tu v direkcii D vektoru (1;1;1) )
ostatne dva su jednodkove vektory vybrane v ortogonalnom priestore na D ( vektorova rovina) . To preto ta otazka co som napisal vysie.
Je dolezite vediet, ako by sa to vyjadrilo v stardnej baze.

Uvedom si , ze tento princip :Vseobecne na urcenie "vektorovych" aplikacii staci urcit obraz jednej bazy
cf ↑ vanok:
to pouzil aj kolega v jeho poznamke ↑ LukasM:

Posledna poznamka: nezabudni ze je vzdy nutne vediet v akych bazach pracujes!

erzebet · 28. 05. 2012 22:46

Chcela by som sa spýtať ako na úlohu typu:
V štandardných súradniciach v R3 napiste maticu zobrazenia, ktora je symetriou podľa roviny sqrt(3)*y-x=0
Viem že treba najst bazu v ktorej najdem maticu zobrazenia typu
{
a ze alfa bude Pi
a ta baza :
kde =(sqrt(3)/2,1/2,0)
=(1/2,-sqrt(3)/2,0)
=(0,0,1)

Poradíte mi?

Matematické Fórum

#1 26. 05. 2012 18:27

Matice symetrie

#2 27. 05. 2012 10:08 — Editoval LukasM (27. 05. 2012 10:09)

Re: Matice symetrie

#3 27. 05. 2012 12:09

Re: Matice symetrie

#4 27. 05. 2012 12:55

Re: Matice symetrie

#5 27. 05. 2012 13:10

Re: Matice symetrie

#6 27. 05. 2012 13:20 — Editoval Aquabellla (27. 05. 2012 13:29)

Re: Matice symetrie

#7 27. 05. 2012 16:54

Re: Matice symetrie

#8 27. 05. 2012 17:16

Re: Matice symetrie

#9 27. 05. 2012 18:02

Re: Matice symetrie

#10 27. 05. 2012 18:43

Re: Matice symetrie

#11 27. 05. 2012 19:20 — Editoval vanok (27. 05. 2012 19:21)

Re: Matice symetrie

#12 28. 05. 2012 22:46

Re: Matice symetrie

Zápatí