Matematické Fórum

Neony · 04. 06. 2012 14:01

Dobrý den, chtěl bych se zeptat, jestli by nebyl někdo tak hodný a nepomohl by mi s daným zadáním (důkazem) :

Předem děkuji za pomoc

vanok · 04. 06. 2012 20:20

Ahoj ↑ Neony:,
Napisem ti tu dokaz v dimenzii 3
( a sam si ho upravis na tvoj priklad)

Ak x; y; z su LN
tak 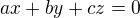$ax+by+cz=0$ ==> $a=b=c=0$

Uvazujme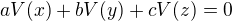
$aV(x)+bV(y)+cV(z)=0$
akoze V je lin aplikacia
mame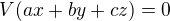
$V(ax+by+cz)=0$
No V je injektivne
tak 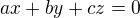$ax+by+cz=0$
co nam da $a=b=c=0$
Konkluzia: 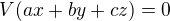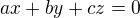$V(ax+by+cz)=0$ ==> $ax+by+cz=0$ , co znamena, ze
V(x);V(y); V(c) su LN.
......
opacna inkluzia
Predpokladajme, ze V(x);V(y); V(c) su LN.

Uvazujme 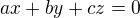$ax+by+cz=0$
co nam da 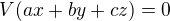$V(ax+by+cz)=0$
akoze V je lin aplikacia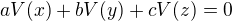
$aV(x)+bV(y)+cV(z)=0$
Vdaka predpokladu

Autor skryl část textu. Zobrazit/skrýt!

mame preto $a=b=c=0$
Konkluzia: $ax+by+cz=0$ ==> $a=b=c=0$
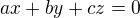co znamena que x; y; z su LN.
...;
Prestuduj si toto pozorne a sa snaz pochopit ako funguje tento dokaz.

Neony · 04. 06. 2012 23:16

Ještě než bych se to snažil aplikovat na svůj případ, rád bych si vyjasnil pár tvrzení. Tak co mi je nejasné je toto: 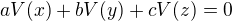$aV(x)+bV(y)+cV(z)=0$ v souvislosti s dalším tvrzením, pokud by toto tvrzení platilo, tak by aditiva měla dle mého názoru vypadat takto: 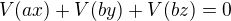$V(ax)+V(by)+V(bz)=0$ a potom bych souhlasil s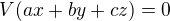 $V(ax+by+cz)=0$
Děkuji za reakci a případně se omlouvam za hloupé dotazy...

vanok · 05. 06. 2012 00:18

Ano, ak pises vsetko detaily tak to treba napisat
Ja som pisal klucove veci

Matematické Fórum

#1 04. 06. 2012 14:01

Důkaz LNZ zobrazení vektorů

#2 04. 06. 2012 20:20

Re: Důkaz LNZ zobrazení vektorů

#3 04. 06. 2012 23:16

Re: Důkaz LNZ zobrazení vektorů

#4 05. 06. 2012 00:18

Re: Důkaz LNZ zobrazení vektorů

Zápatí