Matematické Fórum

Saturday · 15. 11. 2008 13:25

http://kam.mff.cuni.cz/~pultr/ma.pdf - na str. 112 (stránkování dokumentu; popř. str. 116 stránkování PDF) je na posledním řádku na stránce uvedeno, že daná rovnice platí pro j = 1, ..., k (což je jasné, protože mám rovnice 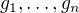$g_1, \ldots, g_n$ už v zadání). 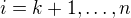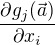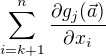Na konci řádku je však uvedeno, že $i=k+1, \ldots, n$ a já nevím, jestli je to jen pomůcka, abych nemusel psát do rovnice (2) místo $\frac{\partial g_j(\vec a)}{\partial x_i}$ sumu $\sum_{i=k+1}^{n}\frac{\partial g_j(\vec a)}{\partial x_i}$ , a nebo jestli to znamená ještě něco jiného? Osobně se kloním k tomu usnadnění zápisu se sumou, protože by to sedělo s tím, že rovnice (2) má být parciální derivace funkce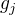 $g_j$

Díky za pomoc

kaja.marik · 15. 11. 2008 20:59

Me prijde, ze to omezeni od k+1 do n se objevuje uz na tretim radku dukazu.

Ale nemam to ted cas nejak podrobneji studovat, tak bych prozatim jenom dodal, ze to mozna bude k dogoogleni jako metoda Lagrangeovych multiplikatoru (a treba se povede najit dukaz, kterry je zrejmejsi).

kaja.marik · 23. 11. 2008 19:00

Nejak jsem se k tomu zapomnel vratit. Je to porad aktualni?

Saturday · 23. 11. 2008 19:05

↑ kaja.marik: Ano, je (potrebuji si to vyjasnit pred zkouskou).

> Me prijde, ze to omezeni od k+1 do n se objevuje uz na tretim radku dukazu.
myslim, ze kdyz se to vyjasni na jednom miste, tak se to vyjasni i na tom druhem :-)

kaja.marik · 23. 11. 2008 20:33

Ja porad moc nechapu dotaz, ale myslim ze to souvisi s tim, cemu rikaji fyzikove stupen volnosti: Kdyz mam tricet promennych a deset nezavislych vazebnich podminek, ma soustava dvacet stupnu volnosti - dvacet promennych se muze nejak menit (napriklad pro ne muzu definovat pocatecni podminky) a zbytek vyplyne z tech vazebnich podminek.

Dal by se pro jistotu dotaz zformulovat takto:

Na ..... radku v dukazu je ........, ale ja bych tam cekal ........

Saturday · 23. 11. 2008 20:49

Rozumím tomu, co je vázaný extrém, že je to hledání extrému za nějakých podmínek (rovnic v tomto případě).

Na poslednim radku na strane 112 je 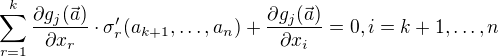$\sum_{r=1}^{k} \frac{\partial g_j(\vec a)}{\partial x_r} \cdot \sigma_r'(a_{k+1},\ldots,a_n) + \frac{\partial g_j(\vec a)}{\partial x_i} = 0, i = k + 1, \ldots, n$ (1), ale ja bych tam cekal $\sum_{r=1}^{k} \frac{\partial g_j(\vec a)}{\partial x_r} \cdot \sigma_r'(a_{k+1},\ldots,a_n) + \sum_{i=k+1}^{n}\frac{\partial g_j(\vec a)}{\partial x_i} = 0$

Je to tak? Nebo jde o n - (k + 1) rovnic tvaru (1)?

kaja.marik

↑ Saturday:
je to vic rovnic.

Zkusme třeba toto (pro ilustraci, možná tohle konkrétní zadání při počítání nebude dávat smysl, nevím)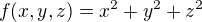
$f(x,y,z)=x^2+y^2+z^2$

$g_1(x,y,z)=x+y-z-1$
$g_2(x,y,z)=x+2y-z-5$

Priklad 1. Pokud hledám vázaný extrém při vazební podmínce g_1=0, můžu z g_1=0 vypočítat x s f bude funkce jenom dvou proměnných: y,z

Priklad 2. Pokud hledám vázaný extrém při vazebních podmínkách g_1=0, g_2=0, vypočítám podobně x a y pomocí z a f bude vlsatně jenom funkcí proměnné z

Takto se "zbavím" prvních k proměnných v první větě důkazu. Zůstanou tam tedy proměnné od 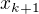$x_{k+1}$ do $x_n$ (tj. y,z v nasem prvnim priklade, a jenom z ve druhem priklade) a pracuju s tim jako s funkci (n-k) promennych - zderivuji podle (n-k) promennych, derivace polozim rovny nule a mam (n-k) rovnic --- pozor, tech rovnic je n-k, ne n-(k+1).

Pri tom derivovani podle kterekoliv z poslednich (n-k) promennych uz vim, ze prvnich k promennych zavisi na tech (n-k) n akonci a beru to tedy jako slozenou funkci, to je to XII.3.2

Hm, ted se koukam, ze jsem vysvetloval to k+1..n v (1), ale dotaz byl na (2) :(

Na dalsi strance se vezme reseni prvnich k rovnic a dokazuje se, ze plati i rovnice od indexu k+1 do n. K tomu potrebuju i derivace funkci g_j podle x_{k+1}, x_{k+2} atd.

Funkce g_j zavisi na n promennych, prvnich k ale neni volnych, jsou vyjadrit pomoci poslednich (n-k) promennych, ktere jsou nezavisle. Kazda volna promenna ev funkcich f a g je tedy obecne jeste "schovana" i v kazde vazane promenne.

napriklad v Priklade cislo 1 je funkce f=(1+z-y)^2+y^2+z^2 --- z se díky vazební podmínce objevilo v členu, který "patřil první proměnné x"

Funke g je konstatni (tak je formulovana vazebni podminka) a jeji derivace podle kazde nezavisle promenne je proto rovna nule. A derivace podle nezavisle promenne je rovna parcialni derivaci (to je ten druhy clen na leve strane rovnice (2)) a podle pravidla pro derivaci slozene funkce tam jsou jeste vsechny cleny, kde ta promenna je "schovana" - a ona je schovana prave v tech prvnich k promennych. Proto tam je jeste derivace podle kazde z tech prvnicch k promennych nasobena tim, jak moc se v teto promenne projevuje ta nezavisla promenna, podle ktere derivujeme.

Je to jasnejsi, nebo to mam zkusit vysvetlit jinak?

Saturday · 23. 11. 2008 22:34

↑ kaja.marik: Děkuju, už chápu :-), já jsem znal podstatu, tedy že jde o vyjadřování proměnných, ale stále jsem dělal jednu hloupou chybu, když jsem to četl *sad*

Matematické Fórum

#1 15. 11. 2008 13:25

Vázané extrémy - problém se zápisem

#2 15. 11. 2008 20:59

Re: Vázané extrémy - problém se zápisem

#3 23. 11. 2008 19:00

Re: Vázané extrémy - problém se zápisem

#4 23. 11. 2008 19:05

Re: Vázané extrémy - problém se zápisem

#5 23. 11. 2008 20:33

Re: Vázané extrémy - problém se zápisem

#6 23. 11. 2008 20:49

Re: Vázané extrémy - problém se zápisem

#7 23. 11. 2008 21:52 — Editoval kaja.marik (23. 11. 2008 22:25)

Re: Vázané extrémy - problém se zápisem

#8 23. 11. 2008 22:34

Re: Vázané extrémy - problém se zápisem

Zápatí