Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 24. 06. 2012 16:34
#3 24. 06. 2012 16:46
#4 24. 06. 2012 17:02
#6 24. 06. 2012 17:24
Re: integrály
Offline
#8 24. 06. 2012 17:57
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: integrály
↑ pololilo:
hale-hale :-)
a) kolegyňka ↑ drabi: zkoušelA (nebo nezkoušelA),
b) můžeš pro kontrolu používat i MAW
A Tvůj výsledek také není noc moc převratného:
vyšlo mi pětina a sedmina...
Používej, prosím, TeX a piš podrobně, co chceš kontrolovat
Offline
#9 24. 06. 2012 18:16
Re: integrály
↑ pololilo:
samozrejme se to da zapsat i jinak, koukni se na show steps.. treba ti to pomuze.
Offline
#10 24. 06. 2012 18:23
Re: integrály
↑ jelena:
jo tak to se nedivím, že se to slečně nechtělo počítat :D ;-)
ten výsledek má vyjít (jedna pětina sinus(na pátou) iks - jedna sedmina sinus(na sedmou) iks), jenže já to počítal, ale pořád mi vychází místo na pátou - našestou, a místo na sedmou - na osmou, tak jestli dělám někde zásadní chybu, řekněte mi to prosím dámy ;-)
Offline
#11 24. 06. 2012 18:30
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: integrály
↑ drabi:
já se omlouvám za vstup, ale mám moderátorskou povinnost přerušit kolegovo slohové cvičení :-)
↑ pololilo:
postupovala jsem  a substituci
a substituci 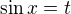 (tedy "na šestou" a "na osmou" se mi jeví reálné).
(tedy "na šestou" a "na osmou" se mi jeví reálné).
Pokud máš nějaký výsledek, zkus ho zderivovat.
A teď už zanechám ve společnosti kolegyňky, děkuji.
Offline
#12 24. 06. 2012 18:32
Re: integrály
Goniometrické funkce mají spoustu možných zápisů jedné a té samé funkce, navíc integrál může být posunutý o konstantu. Takže jestli máš o svém řešení pochyby, tak ho buď zderivuj nebo pokud jsi líný, tak zadej výsledek, který dal wolfram a svůj do jednoho obrázku a pokud budou vypadat stejně, tak jsi počítal správně. Jinak sem musíš dát svoje řešení krok po kroku aby bylo možné najít chybu.
Offline
#14 24. 06. 2012 19:04
Re: integrály
Taky jsem si to spočítal a vyšlo mi to stejně jako tobě. Problém wolframu je, že na některé integrály, které lze velmi zjednodušit vhodnou substitucí využije univerzální vzorec (tady  ).
).
A když zadám obě funkce vykreslit, tak je vidět že jsou až na konstantu stejné.
Offline
#15 24. 06. 2012 19:10 Příspěvek uživatele pololilo byl skryt uživatelem pololilo. Důvod: chyba
#17 24. 06. 2012 19:15
Re: integrály
↑ pololilo:↑ pololilo:
jasne ten robot to počítá špatně, ale to by chtělo aby někdo přišel na to kam se podělo to jedno ,,x'' o který se liší výsledek.
Ten postup co jsem poslal, s tim mi všechny integraly vychazeji.
Offline

