Matematické Fórum

FliegenderZirkus · 25. 06. 2012 15:26

Zdravím, rád bych se zeptal, zda v následujícím odvození derivace inverze tenzoru druhého řádu nenastane problém s tím, že tenzor $\mathbf{A}+t\mathbf{X}$ nemusí být invertibilní, tj. zda bychom neměli uvažovat nějaké omezení na $\mathbf{X}$ a případně jaké.

Podobná otázka je řešena již v tomto odstavci, kde se sice jedná o reálnou funkci tenzorového argumentu, narozdíl od výše uvedené tenzorové funkce tenzorového argumentu, nicméně mělo by to být podobné:

Autor skryl část textu. Zobrazit/skrýt!

Děkuji za reakce.

Rumburak

Ahoj.
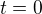Řekl bych, že když tensor $A+ tX$ je invertibilní pro $t = 0$ , pak existuje $\delta > 0$ takové, že uvažovaný tensor
je invertibilní i pro libovolná $t \in (-\delta, \delta)$ . Jde-li o tensory represenované čtvercovými maticemi, plyne důkaz
této věty z faktu, že funkce $f(t) = \det(A+ tX)$ je spojitá (speciálně v nule).

FliegenderZirkus

Perfektní, díky za odpověď. Pokud jde o tu poznámku ve skrytém textu o funkcích definovaných např. jen na symetrických maticích (nebo tenzorech, v tomhle případě to bude podobné), tak ten rozdíl bude v tom, že žádné $\delta > 0$ takové, že pro libovolná $t \in (-\delta, \delta)$ bude vždy $\mathbf{M}+t\mathbf{X}$ symetrická nenajdeme, že? (M je sym., W antisym., X libovolná)

Rumburak

V tom případě musíme za "základní" lineární prostor vzít prostor těch např. symetrických matic (daného typu) ,
takže nejen M, ale též X a M+tX budou symetrické matice.

FliegenderZirkus · 26. 06. 2012 09:40

Bezva, díky za pomoc.

Matematické Fórum

#1 25. 06. 2012 15:26

Derivace ve směru tenzoru

#2 25. 06. 2012 16:08 — Editoval Rumburak (25. 06. 2012 16:09)

Re: Derivace ve směru tenzoru

#3 25. 06. 2012 20:06 — Editoval FliegenderZirkus (25. 06. 2012 20:11)

Re: Derivace ve směru tenzoru

#4 26. 06. 2012 09:11 — Editoval Rumburak (26. 06. 2012 13:28)

Re: Derivace ve směru tenzoru

#5 26. 06. 2012 09:40

Re: Derivace ve směru tenzoru

Zápatí