Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 07. 2012 15:37 — Editoval jarrro (19. 07. 2012 15:41)
Oscilujúce rady
ahojte táto téma spôsobila, že ma napadlo, či pre každý oscilujúci rad (limita postupnosti čiastočných súčtov neexistuje ani vlastná ani nevlastná) a pre každú (aj nevlastnú) hromadnú hodnotu postupnosti čiastočných súčtov existuje uzátvorkovanie, ktorého súčet je tá daná hromadná hodnota ?
MATH IS THE BEST!!!
Offline
- (téma jako vyřešené označil(a) jarrro)
#2 27. 07. 2012 13:05
Re: Oscilujúce rady
↑ jarrro:,
Ahoj, mozes dat nejaky konkretny priklad co ilustruje tvoju myslienku?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 27. 07. 2012 14:48 — Editoval jarrro (27. 07. 2012 14:54)
Re: Oscilujúce rady
↑ vanok:
tak neviem napríklad rad 
má za postupnosť čiastočných súčtov postupnosť
a dá sa uzátvorkovať ako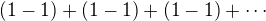 čo má súčet 0, ale aj ako
čo má súčet 0, ale aj ako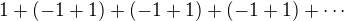 čo má súčet 1
čo má súčet 1
preto ma napadlo či náhodou to tak nie je s každým oscilujúcim radom podobne ako, že neabsolútne konvergetný rad sa dá prerovnať tak, aby bol oscilujúci, s nekonečným súčtom oboch znamienok alebo dokonca mal ľubovoľný reálny súčet.
MATH IS THE BEST!!!
Offline
#4 27. 07. 2012 15:13
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Oscilujúce rady
Ono je rozdil prerovnat (komutativita) a prezavorkovat (asociativita).
viz prvni prispevek
existuje uzátvorkovanie,
a treti
neabsolútne konvergetný rad sa dá prerovnať
S tim prerovnanim rady neco takoveho funguje, byva to v ucebnicich blizko tech partii, ktere se zabyvaji komutativitou u nekonecnych rad
Neco podobneho je http://www.math.muni.cz/~plch/nkpm/ , veta 3.8., Riemannova. Neni to sice presne tohle, ale myslim, ze kdyxz jsme si to pred sto lety na prednasce odvozovali, tak nam z konstrukce bylo jasne, ze radu muzu udelat oscilatorickou s tim, ze limita inferior a superior posloupnosti castecnych souctu jsou jakakoliv dopredu zadana cisla.
Ale jak rikam, jenom si to myslim. Presny dukaz nechavam ctenari jako cviceni, ja tu mam spoustu jinych cviceni .... :)
Offline
#6 27. 07. 2012 16:02
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Oscilujúce rady
↑ jarrro:
Pokud je a hromadný bod posloupnosti částečných součtů 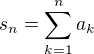 , pak existuje vybraná podposloupnost
, pak existuje vybraná podposloupnost 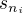 ,
,  z posloupnosti částečných součtů
z posloupnosti částečných součtů 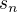 taková, že její limita je
taková, že její limita je 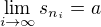 . Z původní posloupnosti uzávorkujeme vždycky členy od indexu
. Z původní posloupnosti uzávorkujeme vždycky členy od indexu  do indexu
do indexu 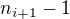 pro
pro  .
.
Nepřemýšlel jsem nad tím dlouho, tak snad neříkám nesmysly :-)
Offline
#7 27. 07. 2012 16:54 — Editoval found (27. 07. 2012 17:01)
Re: Oscilujúce rady
Já se v tom nepohybuji moc dlouho, tak snad nebudu plácat blbosti.
Když ale máme neabsolutně konvergující řadu, potom platí, že 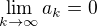 , takže od určitého indexu platí, že
, takže od určitého indexu platí, že 
Což nám jaksi zaručuje, že 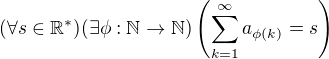 .
.
Takže přerovnání, aby neabsolutně konvergující řada, měla libovolný reálný součet (i nekonečný), existuje.
Co se týče té oscilace, v tom se nevyznám, ale myslím si, že by to mohlo fungovat stejně.
Edit: Myslím, že by se hypoteticky měla dát vytvořit přerovnaná posloupnost, která bude obsahovat dvě podposloupnosti s různými členy, přičemž každá z těchto posloupností bude mít svou limitu.
Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline
#8 27. 07. 2012 17:21
Re: Oscilujúce rady
↑ Pavel Brožek:Diky to ma nenapadloͺ ale asi si chcel napísaťͺ že treba zatvorkovať od indexu 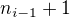 do indexu
do indexu  nie?(
nie?(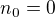 )
)
MATH IS THE BEST!!!
Offline
#9 27. 07. 2012 17:42
Re: Oscilujúce rady
Pozdravujem ↑ jarrro:,↑ Pavel Brožek:,
Pavol, previedol problem tykajuci sa radu na problem postupnosti... a jeho uvaha je spravna pre akukovek radu... cize hypotesa oscilacie nie je potrebna.... a plati aj pre konvegrentnu radu ( i ked neda nic nove v tom pripade)
Poznamka: Pavlova teoria ti ukazuje, postupnost ciastocnych suctov v pripade rady ma hromadne body 0 a 1, cize "zatvorkovanim" nedosiahnes nic ine ako 0 alebo 1 ako limity.
ma hromadne body 0 a 1, cize "zatvorkovanim" nedosiahnes nic ine ako 0 alebo 1 ako limity.
Ako som poznamenal v predoslom vlakne, dalsia moznoznost na limitu takejto rady je napriklad C-limita (limita v zmysle Cesaro )
pozri aj sem
http://en.wikipedia.org/wiki/Ces%C3%A0ro_mean
kde je poradena aj kniha od Hardy.
Ako aj tu kde su dalsie generalizacie pojmu limity:
http://en.wikipedia.org/wiki/1_%E2%88%9 … %B7_%C2%B7
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline