Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 08. 2012 15:48 — Editoval miso16211 (10. 08. 2012 16:00)
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Rovnica postupnosti
Zdravím, po 5 dní som tu znova
5 + 6 + 15 + 16 + 25 + 26 + ... + x = 1221
Má vyjsť 106.
Viem že, sa dajú utvoriť dvojice (5+6) + (15 + 16) ... + x = 1221

vznikne mi tak rovnica
rešením je n = 11
210 /2 = 105 , x = 106
Ale ako by som to mal riešiť ak by x nebolo 106 ale 105.(Postupnosť by končila 105 teda by som urobil dvojice až po x)
napr.
5+6 + 15 + 16 + 25 + 26 + ... + x = 1335 (tu je to po čislo 114)
rovnica by bola 
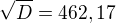 po zaokruhleni
po zaokruhleni
z toho usudim že ku x nemam dvojicu?
ale ako ďalej? Utvorim si ďalšiu dvojicu, teda
5+6 + 15 + 16 + 25 + 26 + ... + x + x + 1 = 1335 + x + 1?
Offline
- (téma jako vyřešené označil(a) miso16211)
#2 10. 08. 2012 23:11
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rovnica postupnosti
↑ miso16211:
Zde bych řekla, že není nejvhodnější zápis, který končí jen x:
5 + 6 + 15 + 16 + 25 + 26 + ... + x = 1221
Vývoji v posloupnosti odpovídá (nebo to musím předpokládat):
5 + 6 + 15 + 16 + 25 + 26 + ... + x+(x+1) = 1221
Jiná možnost je vidět v tomto součtu 2 aritmetické posloupnosti - jedna s 1.členem  , druhá s
, druhá s  . Obě s
. Obě s 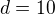
Ale ako by som to mal riešiť ak by x nebolo 106 ale 105.(Postupnosť by končila 105 teda by som urobil dvojice až po x)
Posloupnost nemůže končit 105, neodpovídalo by to "vývoji" podle prvních členů.
5+6 + 15 + 16 + 25 + 26 + ... + x = 1335 (tu je to po čislo 114)
Pokud k 1221 (což je součet 1. posloupnosti dle zadání) přidáš 114 a součet posloupnosti je 1335. Tak co jsi tou 114 přidal? Děkuji.
Offline
#3 10. 08. 2012 23:21
Re: Rovnica postupnosti
Zdravím,
oprav mě, jestli se pletu, ale přijde mi, že zapomínáš, že operuješ s tou "sdruženou" posloupností, takže aby si našel přirozený kořen té kvadratické rovnice, musíš odebrat obě části té sdružené posloupnosti (např. 106 i 105, 96 i 95 atd.). Navíc, proč přičítáš 114, když to není člen žádné z těch posloupností?
Mám pocit, že nechápu úplně tvoji otázku.
Offline
#4 11. 08. 2012 11:28
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: Rovnica postupnosti
↑ Mirgeee:
5 + 6 + 15 + 16 ... + 105 + 106 = 1221
a další člen je 106 + 9 = 114 .
5 + 6 + 15 + 16 + 25 + 26 + ... + x = 1221
je zložena postupnosť, ako ju mam počítať? (ja som ju dal do jednej, tak že urobim vždy po dva dvojice)
Ak mam 5 + 6 + 15 + 16 + 25 = 67 // toto je či nie je postupnost žložená z dvoch aritmetickych?
Sice jedna postupnosť ma o jeden člen viac, ale to by taka uloha nemohla byť?↑ jelena:
↑ jelena:
Ja som myslel, či existuje taka zložená postupnosť, ktorá sa skladá z dvoch aritmetických, pričom prvá postupnosť by mala o jeden člen viac.
napr. 5 + 6 + 15 + 16 + 25 = 67 // sklada sa z dvoch postupnosti,1. 5+15+25
2. 6 + 16
Viem, že som mal označiť 5+ 6 + ... + x + x+1 = 1221 (ak to neurobim x mi vyjde, odpočítam 1 a vydelim dvomia potom ku čislu pripočítam 1)
Asi neviem čo je združená postupnosť(2 aritmetické postupnosti). Musí mať odpovedajúce dvojice čísel?
Offline
#5 11. 08. 2012 12:02 — Editoval vanok (11. 08. 2012 12:04)
Re: Rovnica postupnosti
↑ miso16211:
Ahoj, mas celkom dobru myslienku.
Na toto cvicenie, je najlepsie vyuzit navrh ↑ jelena:, z malym vylepsenim.
Predpokladaj ako ↑ jelena: ktoru tiez pozdravujem
ze 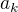

su dve aritmeticke postupnosti ktorych sucet prvuch n clenov je 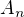 a
a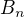
Tvoj problem sa moze teraz napisat takto
Najdite riesenie pre n prirodzene tohto problemu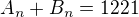 ALEBO
ALEBO
Staci?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
