Matematické Fórum

↑ Mirgeee:

Jistě záleží na dalších proměnných, ty si prosím podle potřeby doplňtě sami.

Problém je právě v této větě, jen s tužkou a papírem se daleko nedostaneme. Buďto si tedy nějaký konkrétní ventilátor vezmeme a proměříme, nebo potřebné údaje vyčteme z katalogu. Když pominu fakt, že na takové měření nejspíš nemáš vybavení, tak by to taky bylo poněkud neefektivní, protože to už bychom rovnou mohli provést celý experiment bez jakýchkoli výpočtů.

Myslím, že tvar vrtule tiež má na to vplyv

Samozřejmě že tvar vrtule má vliv. :-)


Nejjednodušší fyzikální model, který bychom mohli na tuto situaci zkusit napasovat, je proud vzduchu ve směru osy x o určitém průřezu a konstantní rychlosti dopadající na rovinnou stěnu a předávající jí svou veškerou hybnost ve směru x. Takovou situaci lze popsat zákonem zachování hybnosti, který platí i pro tekutiny. Z něj získáme sílu působící na stěnu jako 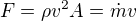, značení je myslím zřejmé. Hlavním problémem tady bude to, že proud vzduchu za ventilátorem je mnohem „širší“ než je plocha bublifuku, ani zdaleka mu tedy nepředá všechnu svou x-hybnost. S tím souvisí druhý problém, a to že rozdělení rychlosti nebude po průřezu konstantní. I kdybychom tedy nějak změřili či odhadli průřez proudu vzduchu , nemůžeme jen tak říct, že , kde A_b je plocha bublifuku. Pro nějaký hrubý odhad by to ale možná takhle stačilo. Pak ještě určit rychlost v resp. hmotnostní tok, což je potřeba učinit z katalogu, s čímž žádnou zkušenost nemám. Nějaký výpočet např. na základě dodávaného elektrického výkonu a odhadnuté účinnosti si moc neumím představit, to už by bylo jak z křišťálové koule. :-)

S mýdlovými bublinami taky žádnou výpočetní zkušenost nemám, po chvilve googlování jsem ovšem našel vzorec, kam by možná mohlo stačit za oba poloměry křivosti dosadit poloměr „tvořítka“ bublifuku, protože po vytvoření polokoule mu budou poloměry křivosti ve všech směrech rovny a povrchové napětí někde vyčíst s vědomím, že chyba bude ve stovkách procent.

Shrnul bych to tak, že každý krok o něco blíže k realitě bude vykoupen velikým nárůstem náročnosti jak co do výpočtů tak co do vybavení, což je nakonec charakteristické pro skoro všechny zajímavé problémy skutečného světa.

Mě by zajímalo, jak je to s hmotností hmoty tvořící bublinu, která podle mě bude nerovnoměrně rozložená. Fyzika to asi ale zanedbá, že?