Matematické Fórum

jarrro · 07. 09. 2012 00:13 — Editoval jarrro (07. 09. 2012 00:13)

ahojte volá sa nejako alebo má nejaký význam funkcia n premenných g, ktorá vznikne z f predpisom
$g{\left(\vec{x}\right)}=\lim_{\vec{t}\to\vec{x}}{\frac{f{\left(\vec{t}\right)}-f{\left(\vec{x}\right)}}{\|\vec{t}-\vec{x}\|}}$
?

Pavel Brožek

↑ jarrro:

Ahoj, nevím, ale nevidím žádné uplatnění pro takovou funkci g. Ta limita existuje jen pokud v bodě x funkce f roste do všech směrů stejně, tj. je v okolí podobná konstatní funkci nebo absolutní hodnotě (pokud je funkce f funkcí jedné proměnné), kuželové ploše (pokud je funkce f funkcí dvou proměnných) nebo nějaké analogické nadploše v případě více proměnných.

Na okolí bodu x je totiž výraz v limitě velmi blízký g(x). Takže pokud limita existuje, tak na okolí x přibližně platí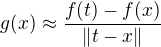

$g(x)\approx \frac{f(t)-f(x)}{\|t-x\|}$

a tedy

$f(t)\approx f(x)+g(x)\cdot\|t-x\|$

jarrro · 07. 09. 2012 00:45

↑ Pavel Brožek:aha to ma len tak napadlo, lebo parciálne derivácie majú uplatnenie, ale nikde sa neuvažuje globálne tú normu som tam dal len, aby malo zmysel delenie proste som chcel niečo čo spraví obraz o celkových pomeroch prírastkov

Pavel Brožek

proste som chcel niečo čo spraví obraz o celkových pomeroch prírastkov

Tak to je totální diferenciál, ne? Není to teda jen jedno číslo, ale těžko asi shrnout chování funkce více proměnných na okolí bodu do jednoho čísla. :-)

Rumburak

↑ jarrro:
Ahoj.
Představ si, že vektorová proměnná 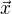$\vec{x}$ je jednodimesionální, tedy $f$ je de facto funkcí jedné (reálné) proměnné.
Potom z výroku

$\lim_{\vec{t}\to\vec{x}}{\frac{f{\left(\vec{t}\right)}-f{\left(\vec{x}\right)}}{\|\vec{t}-\vec{x}\|}} =\lim_{t \to x}\frac{f(t)-f(x)}{|t-x|} = A$

plyne $A = f'_{+}(x)= - f'_{-}(x)$ .

Připadá mi, že hodnota $\lim_{\vec{t}\to\vec{x}}{\frac{f{\left(\vec{t}\right)}-f{\left(\vec{x}\right)}}{\|\vec{t}-\vec{x}\|}}$ pro $\vec{x} \in \mathbb{R}^2$ , pokud by byla definována, by mohla vyjadřovat
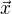něco jako "rotačně souměrnou špičatost" grafu funkce $f$ v bodě $\vec{x}$ (tedy je-li můj geometrický náhled správný) .

EDIT. Vlastně to již jinými slovy vyjádřil kolega ↑ Pavel Brožek:.

jarrro · 07. 09. 2012 11:03

↑ Rumburak:aha a niečo číselné čo vyjadruje "veľkosť" vektora môže byť aj záporné či dokonca komplexnéčo by nahradilonormu a v jednorozmernom by odpovedalo rozdielu?

Rumburak · 07. 09. 2012 11:13

↑ jarrro:

O ničem takovém nevím. Leda snad udělat průmět vektoru do daného směru, ale při tomto zobrazení by i nenulové vektory mohly mít nulový obraz,
což by se Ti patrně nehodilo. Ale je možné, že jsem dobře nepochopil, jak to myslíš.

jarrro · 07. 09. 2012 15:23 — Editoval jarrro (07. 09. 2012 15:28)

↑ Rumburak:ja len nahlas rozmýšľam, že používajú sa parciálne derivácie a matice z nich, ale nikde som nevidel riešiť pomer celkových prírastkov prípadne
ešte ma napadlo dať aj čitateľ do absolútnej hodnoty alebo normy potom by to malo zmysel (ale asi len ten matematický) aj pre vektorové funkcie resp. najprv niečo čo vyjadruje prírastok pri viac rozmeroch pri jednom rozmere je to rozdiel

Matematické Fórum

#1 07. 09. 2012 00:13 — Editoval jarrro (07. 09. 2012 00:13)

názov pre "totálnu deriváciu"

#2 07. 09. 2012 00:34 — Editoval Pavel Brožek (07. 09. 2012 00:38)

Re: názov pre "totálnu deriváciu"

#3 07. 09. 2012 00:45

Re: názov pre "totálnu deriváciu"

#4 07. 09. 2012 00:51 — Editoval Pavel Brožek (07. 09. 2012 00:53)

Re: názov pre "totálnu deriváciu"

#5 07. 09. 2012 09:46 — Editoval Rumburak (07. 09. 2012 10:41)

Re: názov pre "totálnu deriváciu"

#6 07. 09. 2012 11:03

Re: názov pre "totálnu deriváciu"

#7 07. 09. 2012 11:13

Re: názov pre "totálnu deriváciu"

#8 07. 09. 2012 15:23 — Editoval jarrro (07. 09. 2012 15:28)

Re: názov pre "totálnu deriváciu"

Zápatí