Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 09. 2012 12:29 — Editoval peter_2+2 (15. 09. 2012 12:43)
Důkaz toho, že existují tři nekonečna :O
Snad to někomu bude připadat zajimavé.
Začneme Platónem :).
Platón - Faidon str 61, 62
vždyť si ani nevěřím, že když někdo k jednotce přidá jednotku, že se buďto ta jednotka, ke které bylo přidáno, nebo ta, která byla přidána, stala dvojkou, nebo že ta, která byla přidána, a ta, ke které byla přidána, se staly dvojkou přidáním jedné ke druhé;
je mi totiž divné, že když jedna i druhá jednotka byly od sebe zvlášť, byla každá z nich jednotkou a nebyly tehdy dvě, ale když se k sobě vespolek přiblížily, tu se jim tohle stalo příčinou, aby se z nich stala dvojka, totiž to sejití, že byly položeny blízko vedle sebe.
Ani když někdo rozdělí něco, co je jedno, nemohu již míti přesvědčení, že zase to je příčinou, to rozdělení, že vznikla dvojice;
neboť tu se vyskytuje opačná příčina vzniku dvojice než tehdy. Tehdy totiž byla v tom, že se jedno s druhým vespolek sbližovalo a skládalo, nyní že se jedno od druhého oddaluje a odlučuje.
Ani si nemohu zjednati přesvědčení, že vím, čím vzniká jedno, a jedním slovem ani o ničem jiném, čím vzniká nebo zaniká nebo jest při tomto způsobu postupu, nýbrž sám nazdařbůh míchám jakýsi jiný způsob, a tento nijak nepřipouštím.
(str 66, 67, 68)
Proto tedy již nechápu, řekl Sokrates, ostatních příčin, těch učených, ani jim nemohu rozumět; ale jestliže mi někdo říká, proč je něco krásné, totiž že má buď skvoucí barvu nebo krásný tvar nebo některou jinou z takových vlastností, tu si takových výkladů nevšímám - neboť při všech takových výkladech jsem jen uváděn ve zmatek - avšak držím se prostě a neučeně a snad i bláhově té myšlenky, že nic jiného to nečiní krásným nežli buď přítomnost nebo účast onoho krásna, nebo ať už to krásno sem přistoupilo kudykoli a jakkoli; o této věci se totiž ještě nemohu určitě vyslovit, ale o tom ano, že všecky krásné věci jsou krásné krásnem. Neboť toto se mi zdá nejbezpečnější odpovědí i mně samému i jinému; když bych se držel této myšlenky, myslím, že bych nikdy nepadl, a naopak pokládám za bezpečné odpovědět i sám sobě i komukoli jinému, že krásné věci jsou krásné krásnem. Či nezdá se tak i tobě?
.
A tedy velikostí že jsou veliké věci veliké a větší větší a malostí menší věci menší?
Tedy ani ty bys nepřisvědčil, kdyby někdo o někom řekl, že je proti druhému větší hlavou, a ten menší že je právě tímtéž menší. Proti tomu bys důrazně prohlašoval, že ty nesoudíš nic jiného, nežli že všechno cokoli je proti druhému větší, není větší ničím jiným než velikostí, a pro to, pro velikost, že je větší, a co je menší, že ničím jiným není menší než malostí, a pro to, pro malost, že je menší.
Jistě tedy, pravil Sokrates, by ses bál říci, že deset je dvěma více než osm a působením této příčiny nad ono číslo vyniká, a ne že to je množstvím a skrze množství; a dvouloketní míra že jest polovicí větší než loket a ne velikostí - to je jistě asi tatáž obava.
A jistě by ses měl na pozoru, abys neřekl, že když se k jedné přidá jedna, že příčina vzniku dvou je to přidání, nebo když se jedna rozpůlí, to rozpůlení? A hlasitě bys volal, že nevíš, že by každá jednotlivá věc vznikala nějak jinak než tím, že nabude účasti ve vlastní jsoucnosti každého jednotlivého jsoucna(zde, snad, jsoucno velikost - množství), v kterém právě má účasat, a tak i v těchto případech že nemůžeš uvésti žádnou jinou příčinu vzniku dvou nežli nabytí účasti v dvojce; té že se musí státi účastny ty věci, které mají býti dvě, a jednotky to, cokoli má být jedno, ale tohle "rozdělování(z en verze, v cz "rozpůlování") a přidávání" a ostatní takovéto chytrosti bys nechal být a ponechal bys takové odpovědi těm, kteří jsou tobě moudřejší.
==============================================================
A teď by se hodilo trochu odpočinku :). A tak si pojďme ukazovat, jak tedy může vzniknout z jednoho mnohé rozdělováním a mnohé pomocí přidáváním toho, co je jedno.
Takže mějdme na začátku cosi jedno, nějaké množství, třeba délku a označme to jako 1 a jistě pokud vezmeme více jedniček, vznikne nám nějaký počet a tedy mnohé a tak nechme například zprvu vzniknout číslo 3 díky 1+1+1 a netvrďme tedy, aby se nanás Platón nehoršil, že 3 je 3 díky přidávání, ale díky vlastní podstatě sama sebe, uveďme třeba čistou doměnku, že tři je tři díky počtu tří, že jsou zde tři a tak podobně také 5 a také 7 a také 50 a také 90000 a z jednoho nechme vznikat mnohé.
A takto klidně nechme vzniknout nekonečno.
A teď se zase obraťme a mějme nějaké množství a řekněme, že je jedno, tedy 1 a dělme ho na části, jakobychom krájeli nožem, a tak nechme vzniknout z prvu 3, a opět netvrďme, že 3 najednou vznikne krájením, ale že tři má svoji vlastní podstatu, opět uveďme onu doměnku, že tři je tři díky jakýmsi třem, které při něm jsou. A takto tedy nechme z jednoho vznikat opět mnohé rozdělováním a to 5 nebo 8 nebo 999 nebo třeba i nekonečno.
A tak vidíme, že počet nemusí vznikat pouze přidáváním, ale také rozdělováním, anižbychom hledali pravou podstatu toho proč je počet počtem.
==============================================================
A vezměme si dvě množství a hledejme mezi nimi poměr. A nechme ten poměr být například 3násobný.
A __ __ __ B __
A tak jedno množství je pro něco trojkou a druhé pro něco jedničkou, avšak podívejme se nato tak, jakoby i samo první množství bylo pro cosi jedno a i druhé by bylo pro cosi jedno a takto obě množství opakujme stejným způsobem, tedy pokud z prvního jakožto jednoho uděláme 5, udělejme i z druhého jakožto jednoho 5.
5*A =C 5*B = D
__ __ __ __
__ __ __ __
__ __ __ __
__ __ __ __
__ __ __ __
A jistě si všimneme, že přes zvětšení obou množství C=5*A; D=5*B stále bude C trojnásobné proti D a naopak D bude jedna ze tří částí (třetinou) proti C, a že mezi původním množstvím A a B je stejný vztah jako mezi C a D.
A připusťme tedy, že tento vztah je vzájemný:
A B
__ __ __ __
C D
__ __ __ __
__ __ __ __
__ __ __ __
__ __ __ __
__ __ __ __
A tedy pokud jsou A a B k sobě trojnásobné stejně jako C a D jsou k sobě trojnásobné, pak snad již vidíme, že pokud z A uděláme 5 přidáváním jednotek k jednotkám a z B uděláme 5 přidáváním jednotek k jednotkám, tak vztah mezi nimi bude stejný, a že vzhledem k vzájemnosti také platí --->
že pokud nyní pohlédneme na C jako na jednotku a na D jako na jednotku, že pokud C rozdělováním třeba do 5ti částí a D rozdělováním do 5ti částí opět necháme vytvořit číslo 5, pak je vidět, že stejně jako C a D jsou k sobě trojnásobné, stejně tak ona jedna z 5ti částí množství C(=A) a jedna z pěti částí D(=B) budou k sobě opět trojnásobné.
Tedy z matematiky víme, že A a B pokud má k sobě poměr 3:1, pak i 5*A i 5*B k sobě bude mít poměr 3:1.
Stejně tak pokud C a D má k sobě poměr 3:1, pak i C/5 i D/5 k sobě bude mít poměr 3:1.
=================================================================
A tak tedy vezměme si opět čísla 3 a 1 a připusťme, že 3 je trojnásobné proti 1 a kdo tvrdí opak, by nesměl věřit vůbec v principy matematiky.
A kdyby někdo tvrdil, že nekonečno×3 a nekonečno×1 vlastně neexistují, pak jak by vlastně mohl tvrdit, že nekonečno×3 a nekonečno×1 má k sobě poměr 3/1 pokud by neexistovalo jedno nekonečno a trojnásobné nekonečno.
A tedy nechme ty co pochybují pochybovat a podívejme se znovu na 3 a 1 a rozdělujme je na části; tři i jedna rozdělujme zprvu na dvě části a tu se nám ukáže že ony části si jsou stále trojnásobné, rozdělme to na 4 částí a znovu se ukáže, že si jsou k sobě trojnásobné a rozdělme to na nekonečno částí, a stále si budou trojnásobné. A tak tedy pokud nevěříme, že existují něco třikrát větší proti něčemu, co považujeme za nekonečno, jak pak můžeme vůbec věřit, že trojka i jednička jde dělit do nekonečna částí, protože nutně jejich nekonečno částí, díky tomu, že každá z nich je k sobě trojnásobná, díky tomu existují i čísla 3 a 1, které jsou k sobě trojnásobné, a pokud uznáme toto, již by bylo velkým podivem neuznat, že musí existovat nekonečno×3 což je evidentně 3krát větší než nekonečno×1.
A skoro se tedy zdá, že by měli 3nekonečna existovat.
Offline
#2 15. 09. 2012 23:19
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Důkaz toho, že existují tři nekonečna :O
... a pokud by si někdo na toto téma chtěl přečíst nějaký smysluplný text, dobrým výchozím bodem může být http://en.wikipedia.org/wiki/Cantor%27s … l_argument
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#3 16. 09. 2012 14:44
Re: Důkaz toho, že existují tři nekonečna :O
Pozdravujem,
Precitat si aj toto, moze tiez byt zaujimave:
http://fr.wikipedia.org/wiki/Infini
Je to uzitocne citanie.
Pripominam len , ze v modernej matematike a v matematickej logike, pojem nekonecno nema ten isty vyznam ako v beznej reci, ani taky ako v inych vedach, ci aktivitach ktore ho pouzivaju ( napr. fyzika, filozofia, teologia, historia vied...)
Kolega ↑ Kondr:, ukazuje v odkaze na wikipediu na niektore Cantorov-e prispevky, co sa tyka tohto pojmu ( presnejsie: argument diagonaly) v modernej matematike, ktore su pre nu nevyhnutne.... a naviac, priviedli k novym otazkam ako : hypoteza continua...
A tiez v tom odkaze na wikipedii najdete, aj stopu o tom, ake otazky sa daju polozit na tuto temu, v fascinujecej teorii mnozin NF od Quine ( ktora je stale objektom dnesnodobych studii).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 16. 09. 2012 21:27 — Editoval peter_2+2 (17. 09. 2012 05:49)
Re: Důkaz toho, že existují tři nekonečna :O
↑ vanok:
Jenom upozorňuji, že filosofie je láska k pravému poznání a poznávání věcí (nebo taky láska k moudrosti, láska k vědění...).
Čili člověk co hledá pravého poznání v matematice filosofuje a je filosofem. To jen tak k pravému významu slova filosofie, všiml jsem si totiž, že ho dost lidí nesprávně interpretuje.
Pokud tedy tvrdíš, že je tu jakýsi problém v pojmenovávání a ve jméně onoho nekonečna v oborech jako je fyzika a vlastně všechny ostatní vědy mimo matematiky, budu rád, když popíšeš, jak vlastně vypadá pojem nekonečna v matematice, jak vypadá ve fyzice, jak v historii věd (filosofii vynecháme to jsem už vysvětlil, že jenemožné) a teologii. Určitě to bude lidi zajímat - předpkládám, že o těchto věcech máš nějaké mínění, nebudeme hned chrlit tak silná slova jako je vědění, jinak by jsi přece ani nemohl napsat to co jsi napsal, kdyby jsi vlastně vůbec nemínil, že tu nějaký rozdíl je, a že se ti zdá, že jsi jej u těchto věd rozeznal jako odlišný -, ale založ na to když tak prosím nové téma, zdá se mi totiž, že taková věc by měla být oddělena, aby se k ní mohli lidi vyjadřovat odděleně a dostalo se jí tak patřičné pozornosti, jak by si jistě taková věc zasloužila.
Offline
#5 17. 09. 2012 13:26 — Editoval vanok (17. 09. 2012 13:27)
Re: Důkaz toho, že existují tři nekonečna :O
↑ peter_2+2:,
Ahoj, mas prvky odpovede v odkaze co som dal sem ↑ vanok:.
Moja poznamka sa tyka najma toho aby bolo upresnene o ake "nekonecno" ti ide. ( na co si odpovedal v tvojom prispevku)
Osobne nemam cas diskutovat o matematickych pojmoch, co neznamena, ze nemam na to nejaky nazor, ale ide o velmi delikatne veci, v ktorych kazde slovo, ci vyrok moze byt inac interpretovany ako to co by som chcel vyjadrit....
No iste sa na tuto temu vyjadria ini kolegovia, ktory sa tejto teme venovali a daju ti ceske ci slovenske bibliografie. ( Osobne taku literaturu v tych jazykoch nepoznam)
Mala poznamka:
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 17. 09. 2012 16:21 — Editoval anes (17. 09. 2012 16:22)
Re: Důkaz toho, že existují tři nekonečna :O
Ahoj. ↑ peter_2+2:
Jsi na matematickém fóru, tak opatrně se slovem "důkaz".
Asi nejsem dostatečně vybavený, abych ten příspěvek chápal celý, ale snad rozumím poslednímu odstavečku. Tam píšeš, že by měly být aspoň 2 nekonečna, jedno "třikrát větší" než druhé.
Z pohledu "běžné" matematiky je ale obojí jedno a to samé nekonečno. Přirozených čísel je stejně jako čísel celých, jako čísel racionálních, jako čísel tvaru 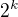 i jako čísel tvaru
i jako čísel tvaru  (to je asi to, s čím nesouhlasíš). Na podrobnější info se dostaneš třeba přes tu wiki.
(to je asi to, s čím nesouhlasíš). Na podrobnější info se dostaneš třeba přes tu wiki.
Můj matematický pohled na věc ale vychází hlavně z toho, že matematika podle mě není v definicích. Matematika se schovává v tvrzeních a zajímavých nápadech a souvislostech. Definice jsou jen makra, aby člověk nemusel pořád sáhodlouze opisovat to samé, co do nich člověk vloží je na něm. Pokud se "náhodou" shodují s nějakou běžnou představou, je to jen dobře, ale to už nechápu jako věc matematiky. Od toho je podle mě právě ta filosofie, fyzika, atd., aby řekly "Hele, tohle se nám hodí. To vypadá, že takhle půjde popsat dráha letící dělové koule, a to nám řekne, kolik každému zbyde koláče potom, co ho rozkrájíme."
Pokud ti někde přijde praktičtější mít nekonečen třeba 50 a podaří se ti to skutečně korektně zavést, směle do toho. Pokud to bude k něčemu dobré, tak třeba přesvědčíš i ostatní, aby na to přistoupili.
Matematika, narozdíl od většiny těch dalších věd, totiž není v principu hádavá. Co jednou platí, to platí pořád. Ano, můžeš vyjít z jiných předpokladů, jinak si zadefinovat pojmy, dojít k jinému tvrzení. Ale tím nijak nezpochybníš to původní. Nekteré definice mohou lépe odpovídat našim představám, některé usnadní prácí, ale neexistuje něco jako "správná" definice.
Takže můj matematický pohled na nekonečno je ten, že to je nějaké označení pro "ne-konečno". Co se týče přesnějších představ, otázek jako kolik jich je, jak s nimi operovat -- beru cokoliv, co se mi zrovna hodí do krámu. Zatím to vždy odpovídalo tomu, co najdeš na wiki, ale v principu se nebráním ničemu.
Offline
#7 23. 09. 2012 15:42 — Editoval peter_2+2 (23. 09. 2012 15:46)
Re: Důkaz toho, že existují tři nekonečna :O
↑ vanok:
Ahoj, třeba tou diskusí objevíš nové věci :o.
↑ anes:
Ahoj.
Nechápu, jak může být celých čísel stejně jako racionálních. Vždyť mezi 1/1 a 3/1 leží jen jedno tak zvaně číslo celé 2/1 a tak zvaně racionálních čísel mezi nimi leží nespočet, skoro si troufám říct nekonečno. (jinak neumím francouzsky bohužel)
S tímto (jako čísel tvaru 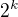 i jako čísel tvaru
i jako čísel tvaru  ) bych i souhlasil, vždyť pokud například "k" bude 5 různých tak zvaně čísel, tak i 2^k musí dát vzniku jakýchsi 5ti.
) bych i souhlasil, vždyť pokud například "k" bude 5 různých tak zvaně čísel, tak i 2^k musí dát vzniku jakýchsi 5ti.
Není diferenciální počet založen na tom, že dělí jedničku do nekonečna částí, z nichž jedna tato část se označuje jako dx? A není pak nutně i diferenciální rovnici nutno přejít 2nekonečna, aby přešla o +1+1 na xové souřadnici? Nebo snad pokud je nekonečno vždy jedno a totéž, pak si náhodně vyberu, zda při součtu nekonečna částí se dostanu na xové souřadnici o jedničku dál nebo o dvojku dál nebo o nekonečno dál?
Těmto věcem tedy moc nerozumím, ale v tomto jsi se podle mě dopustil omylu:
(k pojmu filosofie abych v tom zase nešťoural, tak řeknu, že to co považuji já za filosofii je ta antická, tedy láska k poznání a každý tak zvaně dnes vědec musí být podle mě filosof, pokud nedělá svoji práci v převážné míře z donucení...
K tomuto:
Matematika, narozdíl od většiny těch dalších věd, totiž není v principu hádavá. Co jednou platí, to platí pořád.
Na to se dá snadno tázat, jak matematika došla na to co platí, leželo to na zemi nebo to všichni z ničeho nic jednomyslně uznali, nebo to byla věc sporu.
Pokud jsi myslel to, že je jedna věc považovaná za dokázanou a na nic se navazuje, takových by se našlo spousta. Divil by ses, které věci dnes považujeme za samořezjmé, přesto dřív museli být objeveny jako plod filosofie, třeba to že existuje nějaká gravitace, to že každá věc nemá tělo, jak se dřív někteří domnívali nebo že nemoci nepocházejí ze špíny atd atd atd.
Offline
#8 23. 09. 2012 21:32
- Anonymystik

- Příspěvky: 585
- Reputace: 45
Re: Důkaz toho, že existují tři nekonečna :O
↑ peter_2+2:
Ahoj.
O tomto tématu by se dalo mluvit dlouho, takže řeknu asi tolik: s nekonečnem bych byl opatrný, protože bez něj by matematika byla o hodně slabší - nefungovala by mat. analýza (my se snažíme obejít potřebu nekonečna pomocí limit, ale přesto v definici limity je schované potenciální nekonečno - viz. známé "pro libovolně malé epsílon existuje dostatečně malé delta..."). Naproti tomu axiom výběru pracující s nekonečnými množinami vede v důsledku k takovým zvěrstvům jako je Banach Tarského paradox, které nemají žádný obraz v reálném světě (aspoň ne žádný, o kterém bych věděl).
Doporučím na YouTube kanál "njwildberger", kde se profesiální matematik a profesor z Austrálie, Norman Wildberger, pokouší v sérií svých videí přebudovat od základů matematiku tak, jak ji známe. Stejně jako já je tak trochu skeptický k nekonečným množinám a práci s nimi. Nemůžu říct, že bych stoprocentně souhlasil se vším, co říká, ale rozhodně na jeho názorech bude něco pravdy, takže doporučuji shlédnout.
"Do you love your math more than me?" "Of course not, dear - I love you much more." "Then prove it!" "OK... Let R be the set of all lovable objects..."
Offline