Matematické Fórum

Pavel Brožek

Ahoj,

mám regulární hladké zobrazení 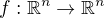$f:\mathbb{R}^n\to\mathbb{R}^n$ , tedy funkce $\vec{y}(\vec{x})$ . Dále mám nějaký bod $\vec{t}$ a vím, že platí

$\frac{\partial^2 y_i}{\partial x_j\partial x_k}\Big|_{\vec x=\vec t}=0$ pro každé i, j, k.

Platí pak nutně pro inverzní zobrazení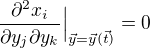

$\frac{\partial^2 x_i}{\partial y_j\partial y_k}\Big|_{\vec y=\vec{y}(\vec t)}=0$ pro každé i, j, k?

Díky za pomoc, nějak mě nic nenapadá, i když to asi bude triviální :-).

Pavel Brožek · 23. 09. 2012 12:11

Je to tak.

Platí (v každém bodě)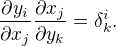

$\frac{\partial y_i}{\partial x_j}\frac{\partial x_j}{\partial y_k}=\delta_k^i.$

To zderivuju podle $x_l$ a dostanu

$\frac{\partial}{\partial x_l}$\frac{\partial y_i}{\partial x_j}$\frac{\partial x_j}{\partial y_k}+\frac{\partial y_i}{\partial x_j}\frac{\partial}{\partial x_l}$\frac{\partial x_j}{\partial y_k}$=0\nl \frac{\partial^2y_i}{\partial x_l\partial x_j}\frac{\partial x_j}{\partial y_k}+\frac{\partial y_i}{\partial x_j}\frac{\partial^2 x_j}{\partial y_k\partial y_m}\frac{\partial y_m}{\partial x_l}=0$

Z předpokladu $\frac{\partial^2 y_i}{\partial x_j\partial x_k}\Big|_{\vec x=\vec t}=0$ mám pak v tom jednom bodě

$\frac{\partial y_i}{\partial x_j}\frac{\partial^2 x_j}{\partial y_k\partial y_m}\frac{\partial y_m}{\partial x_l}=0.$

To vynásobím 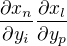$\frac{\partial x_n}{\partial y_i}\frac{\partial x_l}{\partial y_p}$ , vysčítám a dostanu

$\frac{\partial^2 x_n}{\partial y_k\partial y_p}=0,$

což jsem chtěl. :-)

Matematické Fórum

#1 23. 09. 2012 11:40 — Editoval Pavel Brožek (23. 09. 2012 11:41)

Nulovost druhých derivací

#2 23. 09. 2012 12:11

Re: Nulovost druhých derivací

Zápatí