Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » transcendentní číslo (TOTO TÉMA JE VYŘEŠENÉ)
#1 05. 10. 2012 19:30
transcendentní číslo
Ahoj, nějak jsem se zasekla u jednoho příkladu, který máme za úkol.
Dokažte, že je-li číslo  transcendentní, pak je číslo
transcendentní, pak je číslo 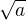 také transcendentní
také transcendentní
nějak mě moc nenapadá, jak na to jít.. koukala jsem se různě po netu a narazila akorát na toto.
Pak jsem přemýšlela nad tím, jestli to nedokazovat nepřímo, že :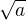 je algebraické, pak i
je algebraické, pak i  je algebraické.
je algebraické.
Akorát jsem s tím nijak nehnula. Mohl by mi prosím někdo poradit? Díky
Offline
- (téma jako vyřešené označil(a) drabi)
#2 05. 10. 2012 23:40
- check_drummer

- Příspěvky: 4637
- Reputace: 99
Re: transcendentní číslo
↑ drabi:
Ahoj, netvoří náhodou algebraciké prvky těleso? A pokdu ano, tak jsou tedy uzavřené na součin...
"Máte úhel beta." "No to nemám."
Offline
#3 06. 10. 2012 08:56
Re: transcendentní číslo
↑ check_drummer:
ahoj, to je možné, ale tuto teorii k dispozici momentálně nemám, přednáška je skoupá na informace:(
Nenapadá tě jiný způsob?
Offline
#4 06. 10. 2012 13:41
Re: transcendentní číslo
stačí ukázať ,že ak je nejaké číslo koreňom polynómu s racionálnymi číslami tak aj jeho mocnina je koreňom polynómu s racionálnymi číslami
napr. pomocou resultantu
konkrétne polynóm s koreňom mocniny (nie nutne minimálny) bude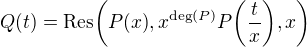
MATH IS THE BEST!!!
Offline
#5 07. 10. 2012 13:37 — Editoval drabi (07. 10. 2012 13:37)
Re: transcendentní číslo
↑ jarrro:
ahoj, díky za reakci.
Koukám teď na to a trochu se v tom ztrácím, pravděpodobně to nějak špatně chápu.
Co se týče definice, tak se tam píše, že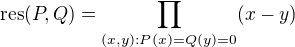
takže například pro tyto polynomy:

by byl 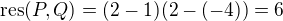
když jsem se koukala i na další wiki odkaz, tak tam se definuje, pomocí determinantu, takže pro náš konkrétní případ:
musela jsem to nějak špatně pochopit, mohl bys mi s tím prosím pomoct?
Offline
#6 07. 10. 2012 14:15 — Editoval jarrro (07. 10. 2012 14:54)
Re: transcendentní číslo
tá matica má byť takto
a napr.
pre prípad racionálneho čísla a
je daný polynóm v tvare resultantu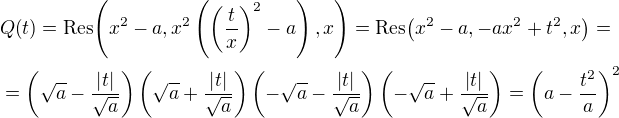
podobne aj pre neracionálne a len miesto polynómu druhého stupňa vziať minimálny(nemusí byť, stačí ľubovoľný s racionálnymi koeficientami, ale zase brať polynóm stupňa milión miesto napr. 4 by bolo odveci) polynóm odmocniny z a. Prípadne sa môže vymeniť t s x, aby výsledný polynóm bol v premennej x, ale to je už len o estetike a nie o logike či matematike
MATH IS THE BEST!!!
Offline
#9 07. 10. 2012 17:16 — Editoval vanok (07. 10. 2012 17:18)
Re: transcendentní číslo
Ahoj ↑ drabi:,
Co sa tyka dokazu tvojej vety
je-li číslo  transcendentní, pak je číslo
transcendentní, pak je číslo 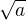 také transcendentní
také transcendentní
v kontrapoznej forme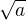 je algebraické, pak i
je algebraické, pak i  je algebraické
je algebraické
som napisal tu
malu poznamku co by ta mohla zaujimat... a to specialne #131.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » transcendentní číslo (TOTO TÉMA JE VYŘEŠENÉ)


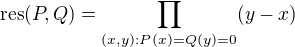
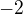 miesto 2 koeficienty sa berú spolu so znamienkom
miesto 2 koeficienty sa berú spolu so znamienkom