Matematické Fórum

JohnPeca18 · 07. 10. 2012 15:40

Ahoj,
tak mam nejake ukoly z pravdepodobnosti, nechci aby to nekdo delal za mne ale dobrou myslenku ocenim.

Zadani:
Bud n>m(log(m+5)). Dokažte, že náhodné zobrazení z [n] (n-prvkova mnozina) do [m] (m-prvkova mnozin) je surjektivní ( je na ) s pravdepodobností alespoň 99%.

Моје myšlenka zatím
Počet všech zobrazení je: 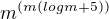$m^{(m(logm+5))}$
Počet surjektivních zobrazení: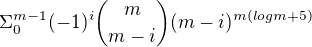 $\Sigma_0^{m-1}(-1)^i\binom{m}{m-i}(m-i)^{m(logm+5)}$
To som teda nejak vystrachal z netu ale nevidim cestu jak ty dva vyrazy podelit.
Jina cesta,:
Pravdepodobnost prvok i z [n] se zobrazi na j z [m] $\frac{1}{m}$
Pravdepodobnost ze prvok i z [n] se nezobrazi na j z [m] je $1-\frac{1}{m}$
Pravdepodobnost ze na prvok j z [m] se nezobrazi ziaden prvok je $(1-\frac{1}{m})^{m(logm+5))}$
Teraz by to chcelo spocitat pravdepodobnost: existuje aspon jeden prvok z [m] na ktory sa nezobrazi ziaden prvok z [n]. Alebo to aspon odhadnut aby to bolo menej ako 0.01.
Moje myslenka dal je to vynasobit m, akoze scitat pravdepodobnosti pre kazdy prvok z [m]
teda:
$m(1-\frac{1}{m})^{m(\ln{m}+5))}\approx me^{-(\ln{m}+5)}=\frac{m}{me^5}=\frac{1}{e^5}\approx$
A to teda je mensie ako 0.01. Hm, tak to mozna bude i spravne :D. Ale kdyz sem si uz dal tu praci, tak to sem napisu. Kdyz tak nekdo na to mrknete jestli ty upravy jsou dobre (najme ten prevod ze na exp, tym sem si nejsi isty). Kdyz tak sem napisu este nejaku inu ulohu. Jano.

Matematické Fórum

#1 07. 10. 2012 15:40

Pravdepodobnost, nahodne zobrazeni

Zápatí