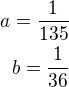Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 10. 2012 15:18
Uloha
Zdravim, prosim poradte, mam jako DU vypocitat tuto ulohu, ale vubec nevim jak nato:
Kdyby práci dělal 1. stroj 93 hodin a 2. stroj 9 hodin, splnily by celkem 169/ 180
úkolu. Kdyby práci dělal 1. stroj 82 hodin a 2. stroj 6 hodin, splnily by celkem
209/270 úkolu. Jak dlouho by úkol plnil 1. stroj sám, jak dlouho by úkol plnil 2. stroj
sám?
Diky Moc
Offline
- (téma jako nevyřešené označil(a) jelena)
#4 14. 10. 2012 18:05
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Uloha
↑ Bugwin:
Zdravím,
neodpovídej si sám, prosím, takové téma se zatoulá. Můžeš označit celé množství úkolu jako u.
Potom hodinový výkon 1. pracovníka je u/x, druhého pracovníka je u/y. Společně splnili nejdřív 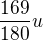 , v druhém případě
, v druhém případě 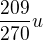 . Tedy můžeme sestavit 2 rovnice (napravo v rovnicích bude splněná část úkolu, jak jsme napsali výš).
. Tedy můžeme sestavit 2 rovnice (napravo v rovnicích bude splněná část úkolu, jak jsme napsali výš).
Označení u používáme jako pomocné, pokud jste ve škole rovnou označovali celou práci za 1, tak ani u není nutné používat.
Teď zapiš, co udělali za odpracovanou dobu: práci dělal 1. stroj 93 hodin a 2. stroj 9 hodin,
a také pro druhou rovnici: práci dělal 1. stroj 82 hodin a 2. stroj 6 hodin.
Tak nám vznikne levá strana pro každou rovnici. Stačí tak? Děkuji.
Offline
#5 14. 10. 2012 18:10
Re: Uloha
↑ Bugwin: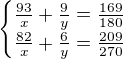
 první stroj sám
první stroj sám druhý stroj sám
druhý stroj sám
OT: a nech si ty ironické poznámky. Lidi tady odpovídají z dobré vůle, nic z toho nemají a můžu tě ujistit, že takovýto krásný slunečný podzimní den si dokážeme najít lepší zábavu, než dělat někomu DÚ
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#6 18. 10. 2012 23:45
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Uloha
↑ zdenek1:
alespoň jsem společné dílo využila na zalepení nevyřešeného tématu. Přitom si myslím, že čas okolo 18:00 je ještě celkem slušný pro umístění návodu k řešení (k debatě o významu umístění v určitý čas :-) Toto také označím za vyřešené, pozdrav.
Offline
#8 09. 01. 2014 11:13
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Uloha
↑ mordok:
Zdravím, v soustavě kolegy ↑ zdenek1: je vhodné použit substituci 1/x=a, 1/y=b, potom je k řešení soustava lineárních rovnic. Stačí tak? Děkuji.
↑ Bugwin:
to by mne zajímalo, za co kolega Zdeněk dostal za toto téma zápornou reputaci? Ozvat se po umístění odpovědi (která byla do 3 hodin od Tvého dotazu), to Tobě nešlo, ale po 1,5 roce dojit se zápornou reputaci - to ano.
Offline
#9 09. 01. 2014 12:30
Re: Uloha
"OT: a nech si ty ironické poznámky. Lidi tady odpovídají z dobré vůle, nic z toho nemají a můžu tě ujistit, že takovýto krásný slunečný podzimní den si dokážeme najít lepší zábavu, než dělat někomu DÚ"
Nevidim nikde abych mel nejake ironicke poznamky.
Offline
#15 09. 01. 2014 16:05
- Peterslovak

- Příspěvky: 270
- Škola: gymnázium
- Pozice: student
- Reputace: 3
Re: Uloha
t1= 135 hodin, t2= 36 hodin.
„Představivost je důležitější než vědomosti.“- Albert Einstein
Offline
#16 10. 01. 2014 00:03
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Uloha
↑ mordok:
Je dobré se naučit tento typ soustav rovnic převáděných na lineární pomocí substituce - v materiálu úplně na závěr (str. 5 a 6 je porovnání metody řešení bez substituce a se substituci). A je vidět, jak je substituce pohodlná v tomto případě.
Možná ještě pomůže přepis tak, aby bylo vidět zlomek pro substituci: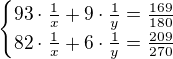
po pouziti 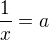 ,
, 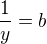 mame soustavu
mame soustavu 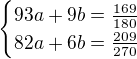
A tu už dořešíš (a na závěr nezapomenout zpět k substituci). Kolegům Cheopovi a Peterslovakovi děkuji za doplnění mezivýsledku a kompletního výsledku.
Offline