Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Vzajemna poloha hyperboly a primky (TOTO TÉMA JE VYŘEŠENÉ)
#1 17. 10. 2012 11:01
Vzajemna poloha hyperboly a primky
1/Určete vzdálenost průsečíků přímky p:4x-3y-12=0 s hyperbolou x^2/9-y^2/4=1
Jsem nasla pruseciky
4x-3y+12=0
x=(3y-12)/4
4x(3y+12/4)^2-9y^2=36
36y=180
y=5
4x-15+12=0
4x=3
x=3/4
Jak ale najdu tu vzdalenost? V tech materialech jsem o ni nic nenasla
2/V průsečících přímky p:x-y+1=0 s hyperbolou (x-3)^2-y^2=16 , napiste obecnou rovnici tecny
Zase teda urcim pruseciky
x-y+1=0
x=+y-1
(y-4)^2-y^2=16
y^-8y+16-y^2=16
y=0
x=-1
Jak ale z nich urcim ty tecny?
Offline
- (téma jako vyřešené označil(a) katulinka)
#2 17. 10. 2012 11:21
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Vzajemna poloha hyperboly a primky
↑ katulinka:
1) Určíš průsečíky hyperboly s přímkou
2) Vzdálenost určíš jako vzdálenost těch průsečíků (vzdálenost 2 bodů)
Nikdo není dokonalý
Offline
#3 17. 10. 2012 11:38 — Editoval Cheop (17. 10. 2012 12:54)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Vzajemna poloha hyperboly a primky
↑ katulinka:
Př.2)
Určíš průsečíky přímky s hyperbolou
2) Tečna k hyperbole procházející tečným bodem T=(x_0; y_0)
bude mít tvar:

Nikdo není dokonalý
Offline
#5 17. 10. 2012 11:51 — Editoval Cheop (17. 10. 2012 11:51)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Vzajemna poloha hyperboly a primky
↑ katulinka:
Z rovnice přímky  vyjádřím x
vyjádřím x a toto dosadím do rovnice hyperboly
a toto dosadím do rovnice hyperboly 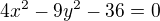
 z tohoto vypočítám y-ove souřadnice průsečíků a následně dopočtu x-ové souřadnice.
z tohoto vypočítám y-ove souřadnice průsečíků a následně dopočtu x-ové souřadnice.
Nikdo není dokonalý
Offline
#6 17. 10. 2012 15:03
Re: Vzajemna poloha hyperboly a primky
↑ Cheop:
Dekuji, toto jsem udelala v mem prvnim prispevku, ale asi chybne. Porad ale me vychazeji jina cisla.
4(3y-12/4)^2-9y^2-36=0
72y=108
y=3/2
Po dosazeni
6-12=3y
y=-2
Navic me vychazi jen 2 cisla, na souradnice P1 a P2 potrebuji 4
Offline
#7 17. 10. 2012 15:25 — Editoval Cheop (18. 10. 2012 09:28)
#9 17. 10. 2012 21:38
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Vzajemna poloha hyperboly a primky
↑ katulinka:
T=(x_0; y_0) jsou souřadnice tečného bodu
v našem přpadě bodu T=(-1; 0)
Nikdo není dokonalý
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Vzajemna poloha hyperboly a primky (TOTO TÉMA JE VYŘEŠENÉ)







