Matematické Fórum

liquid · 27. 10. 2012 23:42 — Editoval liquid (28. 10. 2012 00:11)

Ahoj

snazim se vyresit, jak donutit dva objekty co se pohybuji po balisticke trajektorii stretnout. Vice info dle obrazek.

Mame jeden objekt, ktery jiz leti po trajektorii (na obrazku ta trajektorie co zacina prerusovane).
Na tento objekt pusobi gravitacni zrychleni $g_{a}$ .

V urcitem okamziku 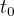$t_{0}$ se rozhodneme hodit dalsi objekt, tak, abychom zasahli objekt puvodni. Na novy objekt pusobi gravitacni zrychleni $g_{b}$ .

Informace ktere mame k dispozici:
$V_{a}$ neboli rychlost puvodniho objektu.
$\alpha$ neboli uhel pod kterym zrovna leti puvodni objekt
(znam totiz velocity objektu ve tvaru [vx,vy], tak tyto dva udaje muzeme snadno dopocitat)
$V_{b}$ - rychlost druheho objektu, neboli jakou rychlosti ho "vystrelim"
$g_{a}$ a $g_{b}$

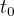ja se snazim spocictat $\beta$ , neboli pod jakym uhlem v case $t_{0}$ objekt vypalit tak, aby zasahl objekt puvodni.

-----------------------------

Pouzil jsem rovnice trajektorie:
$x=x_{0}+v_{x}t$ a $y=y_{0}+v_{y}t-\frac{1}{2}gt^2$
resp. $x=x_{0}+v\cos{\omega } t$ a
$y=y_{0}+v \sin{\omega }t-\frac{1}{2}gt^2$

Snazil jsem se to resit tak, ze vim, ze v 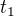$t_{1}$ , budou mit stejny $t$ , stejny $x$ a stejne $y$ .

Bohuzel mi jako neznama neustale zbyva jak cas $t$ , tak uhel $\beta$ .

Pomozete mi s tim, prosim, nekdo?

Pokud se nabizi dve reseni, chci vzdy to s nizsim $t$ (nezapornym samozrejme)

Dekuji L.

jelena · 28. 10. 2012 00:04

Zdravím,

provedu jen korektury:
- gravitační zrychlení je asi stejné, není nutné označovat indexem (a, b)?
- proč je v zápisu $\omega$ , když v textu a na obrázku není?

$y=y_{0}+v \sin{\omega }-\frac{1}{2}gt^2$

- zde chybí $t$ u druhého členu. Tak? Děkuji.

liquid · 28. 10. 2012 00:10 — Editoval liquid (28. 10. 2012 00:12)

↑ jelena:
Ahoj,

$\omega$ tam je jen proto, ze vzorec plati jak pro $\alpha$ tak pro $\beta$ . Mel sem to ale napsat.

Gravitacni zrychleni je opravdu ruzne, prestoze se pohybuji ve stejnem prostoru (jedna se o nerealnou pocitacovou simulaci), tedy $g_{a} \not = g_{b}$

$t$ doplnim

dekuji

zdenek1 · 28. 10. 2012 06:51

↑ liquid:
Ale ty dva parametry ( $t$ a $\beta$ ) ti tam zůstanou vždy.
Informace, že chceš zasáhnout objekt A, sama o sobě nestačí k úplnému řešení. Musíš mít také určeno KDE ho chceš zasáhnout (nebo kdy - což jsou vzájemně převoditelné informace)

liquid · 28. 10. 2012 07:36

chapu, ze kdyz bych mohl se strelou vyckavat, nebo pokud bych mohl vystrelit ruznou rychlosti, tak ze tam nekonecne reseni je. Pokud mam ale pevne dany cas, kdy vystrelit i rychlost jakou vystrelit, nejak tam nekonecne resenich nevidim...

pokud si napr. za $\beta$ zvolim pevny uhel, tak se preci trajektorie protnou max 2x (pokud nejsou totozne) a z toho jen jeden prunik muze mit stejne $t$ . Nebo se pletu?

zdenek1 · 28. 10. 2012 07:50

↑ liquid:

pokud si napr. za $\beta$ zvolim pevny uhel, tak se preci trajektorie protnou max 2x (pokud nejsou totozne) a z toho jen jeden prunik muze mit stejne $t$ . Nebo se pletu?

ALe to je přesně to, co ti píšu. Jeden z těch parametrů si musíš zvolit. Vzhledem k tomu, že v původní otázce jsi chtěl určit $\beta$ , musíš si zvolit $t$ . A není to čas kdy vystřelíš, ale kdy zasáhneš.

nejak tam nekonecne resenich nevidim.

Matce přírodě je to jedno.

Ten úhel nebude naprosto libovolný. Řešení povede na kvadratickou rovnici, a tam bude podmínka pro diskriminant, která dá nějaký interval možných úhlů.

liquid · 28. 10. 2012 08:06 — Editoval liquid (28. 10. 2012 08:06)

ah, diky, chapu jiz jak sem na to blbe nahlizel.

Zkusím tedy zpřesnit, oč mi jde.

Původní objekt proste pouze letí. Druhý objekt, vytřelený pod úhlem $\beta$ se ho snaží zasahnout. Dejme tomu, ze je to delo, ktere muze strilet opakovane (s prodlevou) a chce ho zasahnout co nejvicekrat behem letu. Chci tedy vzdy najit takove reseni, pro ktere bude $t$ minimalni (pokud se nepletu. uhel $\beta$ s tim nema co delat, protoze objekt muze letet bud nahoru ci dolu).

To uz ale vede na derivace a reseni prubehu funkce ne?

Jak na to?

Diky L.

jelena · 28. 10. 2012 09:03

↑ liquid:

potom se mi zdá vhodné vyjádřit $t=f(\beta)$ - "čistý" čas do setkání. Protože úhel lze měnit ve stanoveném rozsahu. Taková závislost se daří sestavit? Děkuji.

liquid · 28. 10. 2012 10:00

no, nejprve resim shodna $x$

$x=x_{0}+v_{x}t$

necht bos stretu je [a,b];

$a=x_{a_{0}}+v_{a}\cos{(\alpha)}t$

$a=x_{b_{0}}+v_{b}\cos{(\beta)}t$

dosazenim do sebe

$x_{a_{0}}+v_{a}\cos{(\alpha)}t = x_{b_{0}}+v_{b}\cos{(\beta)}t$

$t = \frac{x_{b_{0}} - x_{a_{0}}}{v_{a}\cos{(\alpha)}-v_{b}\cos{(\beta)}}$

pokud resim shodna $y$

$y_{a_{0}} + v_{a}\sin(\alpha)t-\frac{1}{2}g_{a}t^2 = y_{b_{0}} + v_{b}\sin(\beta)t-\frac{1}{2}g_{b}t^2$

$t^2(\frac{g_{b}-g_{a}}{2})+t(v_{a}\sin(\alpha) - v_{b}\sin(\beta))+(y_{a_{0}}-y_{b_{0}}) = 0$

kvadr.

$t_{1,2}=\frac{v_{b}\sin(\beta)-v_{a}\sin(\alpha)\pm\sqrt{(v_{a}\sin(\alpha))^2-2v_{a}\sin(\alpha)v_{b}\sin(\beta) (v_{b}\sin(\beta))^2-2(g_{b}-g_{a})(y_{a_{0}}-y_{b_{0}})} } {g_{b}-g_{a}}$

(snad sem pri tom prepisovani neudelal chybu)

ale jak ted dal?

jelena · 28. 10. 2012 10:31

↑ liquid:

tedy máme vyjádřeno $t=f(\beta)$ , zbytek v zápisu jsou známé hodnoty nebo parametry, co umíme počítat pro konkrétní okamžik $v_a$ , $v_b$ .

Potom můžeme zderivovat funkci a určit, pro které $\beta$ je čas minimální.

neztrácíme však ideu úlohy? Já si představuji tak - vyletí objekt a - je zafixován čas výletu, potom mám dostatečnou prodlevu (definovaný čas), ve kterém se úhel $\beta$ nastaví na určitou hodnotu a v určitém okamžiku od výletu objektu a pošlu objekt b. Objekt b poletí minimální čas, který jsme stanovili v předchozím kroku v závislosti na $\beta$ ?

liquid · 28. 10. 2012 10:39

↑ jelena:
cas vyletu objektu a nezname, objekt a proste leti. ja k jeho trajektorii nepristupuju jako k celku (od opravdoveho startu), ale zacnu ho brat jako trajektorii az v dobe vystreleni objektu b. Proto ke srazce maji oba stejne $t$ .

(predpokladam, ze "pootoceni" kanonu na uhel \beta nezabere zadny cas)

jestli se nepletu, tak mi staci pouzivat rovnici, kdy maji shodne $x$ ? tzn zderivovat pouze tu?

jelena · 28. 10. 2012 10:45

↑ liquid:

Objekt a nemůže "prostě letět". Něco o něm vědět musíme - jak ho jinak dáme do souvislosti s objektem b?

Důležité (dle mého) - znám $v_a$ $v_b$ ? Potom můžeme derivovat $t=f(\beta)$ . Ale je možné, že ztrácíme myšlenku.

liquid · 28. 10. 2012 10:52

↑ jelena:

spatne jsem se vyjadril, objekt a leti a ja jsem schopny si v jakykoli cas zjistit informaci o jeho rychlosti (x,y) a pozici.
takze nepotrebuji znat cas kdy vyletel, odkud vyletel, ani rychlost odkud vyletel puvodne. Staci mi v case kdy chci vystrelit projektil b zjistit rychlost objektu a, jeho pozici a tyto informace povazovat jako pocatecni bod a pocatecni rychlost.

Tedy znam 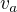$v_{a}$ i $v_{b}$

staci tedy derivovat
$t = \frac{x_{b_{0}} - x_{a_{0}}}{v_{a}\cos{(\alpha)}-v_{b}\cos{(\beta)}}$ ?

Pocatecni pozice znam, rzchlosti znam, uhel alfa znam, jen uhel beta neznam a cas chci minimalni.

jelena · 28. 10. 2012 11:31

↑ liquid:

mně se to nelibí ani trochu. Když to zderivuješ, nic použitelného z toho není. Asi jsme ztratili ideu a budeme doufat, že nás někdo ochotný zachrání.

A my teď a potom poděkujeme.

jelena · 28. 10. 2012 13:39

↑ liquid:

ještě se na to dívám - derivovat pouze t (z vyjádření pro vodorovnou složku) nemůžeme. Jelikož funkci máme zadanou parametricky.

Tedy se bude derivovat vyjádřený výsledek pro t (vidím drobný překlep chybějící +(v_{b}\sin(\beta))^2):

$t_{1,2}=\frac{v_{b}\sin(\beta)-v_{a}\sin(\alpha)\pm\sqrt{(v_{a}\sin(\alpha))^2-2v_{a}\sin(\alpha)v_{b}\sin(\beta)+(v_{b}\sin(\beta))^2-2(g_{b}-g_{a})(y_{a_{0}}-y_{b_{0}})} } {g_{b}-g_{a}}$
v přepisu derivace není složitá (je v tom plno konstant):
$t_{1,2}=\frac{v_{b}\sin(\beta)}{g_{b}-g_{a}}-\frac{v_{a}\sin(\alpha)}{g_{b}-g_{a}}\pm\frac{\sqrt{(v_{a}\sin(\alpha))^2-2v_{a}\sin(\alpha)v_{b}\sin(\beta)+(v_{b}\sin(\beta))^2-2(g_{b}-g_{a})(y_{a_{0}}-y_{b_{0}})} } {g_{b}-g_{a}}$

Jen pořád otázka, zda je to cíl. který jsme potřebovali.

liquid · 28. 10. 2012 14:33 — Editoval liquid (28. 10. 2012 14:34)

↑ jelena:

dekuji za opravu

Mno uz je to nejakou chvilku co sem derivoval, tak sem to radeji nasypal do nejakeho online kalkulatoru...

vypadlo mi z nej toto

tak je to snad dobre.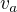

$v_{a}$ = $v$
$v_{b}$ = $w$
$g_{a}$ = $g$
$g_{b}$ = $h$
$y_{a_{0}}$ = $a$
$y_{b_{0}}$ = $b$

ted si nejsem uplne jisty postupem. Musim zjistit kdy je derivace nulova, protoze tam jsou lokalni extremy ze? Pak dosazenim zjistit jestli je na intervalu rostouci/klesajici a dle toho najdu extremy. Mno a nalezene minimum me zajima. To pak jiz dosadim do vzorce pro trajektorii a mam co potrebuji.

Je to tak?

jelena · 28. 10. 2012 15:50

mně to ručně vyšlo trochu jinak (protože nemáš závorku 2*(h-g)*(a-b) na konci prvního řádku:

$\frac{v_{b}\cos(\beta)}{g_{b}-g_{a}}\pm\frac{-v_{a}\sin(\alpha)v_{b}\cos(\beta)+v^2_{b}\sin(\beta)\cos (\beta)} {\sqrt{(v_{a}\sin(\alpha))^2-2v_{a}\sin(\alpha)v_{b}\sin(\beta)+(v_{b}\sin(\beta))^2-2(g_{b}-g_{a})(y_{a_{0}}-y_{b_{0}})}(g_{b}-g_{a})}$

Teď když se dá ke společnému jmenovateli, tak pro nulovou derivaci má být nulový čitatel zlomku.

liquid · 29. 10. 2012 13:43

↑ jelena:

jeleno, diky moc za to, jen to na chvili odlozim, nejak mi zas precvaklo v hlavne to s tim nekonecnym poctem reseni

vezmeme si priklad primek namisto trajektorii, viz. obrazek

sediva cara je objekt, ktery leti (pohled shora) urcitou rychlosti. Z pocatku po nem chci vypalit projektil tak, abych ho zasahl.

v dany okamzik se tedy rozhodnu pro strelbu, tento okamzik pojmenujme t0.

v tom okamziku oznacim misto, kde byl zrovna letici objekt jako bod B. Tento bod budu brat jako vychozi bod pro tento objekt. Uz me nezajima, ze nejakou dobu letel. Proto v dobe stretu budou letet oba objekty stejnou dobu.

Na primku jsem zanesl body, ve kterych bude letici objekt v jednotlivych casech (t1,t2,t3) (konstantni rychlost).
Kruznice naopak udavaji, kde muze byt projektil vystreleny z pocatku v casech t1(cervena) t2(modra) a t3(zluta).

Z obrazku je patrne, ze nehlede na uhel vystrelu v casech t1 a t2 nikdy nemohu zasahnout. Je videt, ze zasah je mozny nekde pred casem t3, teda dejme tomu napr. t2.87. Pro tento cas uz zase existuje ale jeden jediny uhel vystrelu.

Je to tak?
Pokud ano, nejak v tom nevidim, jak se to lisi od trajektorii natolik, ze by meli nekonecne resenich.

pietro · 29. 10. 2012 20:13 — Editoval pietro (29. 10. 2012 21:07)

Ahojte, skúsme doriešiť tie dva šikmé vrhy pre nejaký konkrétny prípad... niečo musíme zvoliť na počiatku...

oprava , ďakujem :-)

liquid · 29. 10. 2012 20:23

↑ pietro:

mno na pocatku znam oba vychozi body (tedy x1 x2 y1 y2)
uhel alfa
obe rychlosti (v1 v2)
i obe gravitacni zrychleni (g1 g2)

znam tedy 9 z 11ti promennych (v2 tam mas 2x)

jelena · 29. 10. 2012 20:49

Zdravím v tématu,

navrhuji ujasnit model: cíl má být zasazen v minimálním čase. Pro tento model už máme $t=f(\beta)$ , přičemž pokud označím různé konstanty (parametry), co máme, tak jedno z vyjádření funkce $t=a\sin\beta+b+\sqrt{(c+d\sin\beta)^2+w}$ a na zvoleném intervalu pro $\beta$ od 0 do 90 je to kus sinusoidy (zřejmě na zvoleném intervalu máme extrém).

tech "nekonečně mnoho řešení" se představuji "nekonečně mnoho bodů" ( $\beta$ , $t$ ), pokud si zvolíme podmínku extrém, tak bod je jeden (pokud nějakou jinou podmínku, tak například budeme mít interval, ve kterém se nachází řešení přijatelné).

Já mám dojem, že toto je standardní úloha, který se musí vyskytovat ve všech střílečkách, bohužel, jsem nikdy žádnou nehrála, ani neprogramovala. Pokud tomu tak není, tak se myslí jiný model, který jsem nepochopila :-)

pietro · 29. 10. 2012 21:14

↑ jelena: Ahoj, Ty už riešiš vyšší level, ja som rád, že som sa trafil v normálnom čase

Odkaz

liquid · 29. 10. 2012 21:20

↑ jelena:

ja sem z toho uplne jalovej :D

uz davno mi bylo jasny to nekonecne moc reseni, ale najednou sem to nejak zapomnel a znova se chyt zvraceny myslenky... zapomnel sem na to minimalni t.

a ano, model chapes naprosto spravne...

a ano, ja opet neco nechapu :) kde sme vzali $t=a\sin\beta+b+\sqrt{(c+d\sin\beta)^2+w}$ ?

jezis me tenhle ukol nejak leze na hlavu... ale doufam ze se nejak doberem k vysledku, tedy k jedne rovnici, do ktere kdyz nasypu tech 9 konstant, tak mi vypadne uhel beta, pod kterym kdyz okamzite vystrelim, tak zasahnu objekt v co nejkratsim case

↑ pietro:
nejak nechapu, jak je toto resenim?

pietro · 29. 10. 2012 22:16

↑ liquid: Ahoj, tu som hľadal čas a rýchlosť pri zvolených alfa a beta

http://www.wolframalpha.com/input/?i=so … -0.5*9*t^2

a tu som hľadal čas a beta pri zvolenom alfa a rýchlosti z prvého výsledku.

http://www.wolframalpha.com/input/?i=so … or+b+and+t

iba zatiaľ testujem či stroj počíta správne... :-)

jelena · 29. 10. 2012 23:45

↑ pietro: :-)

↑ liquid:

to jsem v rychlosti označila konstanty (parametry?). Upravím:
$t_{1,2}=\frac{v_{b}\sin(\beta)}{g_{b}-g_{a}}-\frac{v_{a}\sin(\alpha)}{g_{b}-g_{a}}\pm\sqrt{$\frac{v_{a}\sin(\alpha)}{g_{b}-g_{a}}-\frac{v_{b}\sin(\beta)}{g_{b}-g_{a}}$^2-2\frac{y_{a_{0}}-y_{b_{0}}}{g_{b}-g_{a}}}$

Označím:

$\frac{v_{b}}{g_{b}-g_{a}}=c$
$-\frac{v_{a}\sin(\alpha)}{g_{b}-g_{a}}=k$
$-2\frac{y_{a_{0}}-y_{b_{0}}}{g_{b}-g_{a}}=n$

A je uklízeno (asi tak, jak poznamenal můj milý syn po mém úklidu v reálu "Jaký význam to má, když potom Ty jediná víš, kde co leží" :-)):

$t_{1,2}=c\sin(\beta)+k\pm\sqrt{$k-c\sin(\beta)$^2+n}$

Dokonce nám sedí rozměrnost a v této podobě můžeme i derivovat.

Teď když budeš volit parametry (kterým říkáš konstanty), tak z 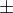$\pm$ se vybere tá varianta, který bude dávat čas nezáporný.

Jak jsme tak přeznačili konstanty, tak např. je vidět, že $-\frac{v_{b}}{v_{a}\sin(\alpha)}=\frac{c}{k}$ , tedy vstupní hodnoty ještě můžeš dávat do poměru. Tak se uvidí :-)

Matematické Fórum

#1 27. 10. 2012 23:42 — Editoval liquid (28. 10. 2012 00:11)

Stret dvou objektu leticich po trajektorii

#2 28. 10. 2012 00:04

Re: Stret dvou objektu leticich po trajektorii

#3 28. 10. 2012 00:10 — Editoval liquid (28. 10. 2012 00:12)

Re: Stret dvou objektu leticich po trajektorii

#4 28. 10. 2012 06:51

Re: Stret dvou objektu leticich po trajektorii

#5 28. 10. 2012 07:36

Re: Stret dvou objektu leticich po trajektorii

#6 28. 10. 2012 07:50

Re: Stret dvou objektu leticich po trajektorii

#7 28. 10. 2012 08:06 — Editoval liquid (28. 10. 2012 08:06)

Re: Stret dvou objektu leticich po trajektorii

#8 28. 10. 2012 09:03

Re: Stret dvou objektu leticich po trajektorii

#9 28. 10. 2012 10:00

Re: Stret dvou objektu leticich po trajektorii

#10 28. 10. 2012 10:31

Re: Stret dvou objektu leticich po trajektorii

#11 28. 10. 2012 10:39

Re: Stret dvou objektu leticich po trajektorii

#12 28. 10. 2012 10:45

Re: Stret dvou objektu leticich po trajektorii

#13 28. 10. 2012 10:52

Re: Stret dvou objektu leticich po trajektorii

#14 28. 10. 2012 11:31

Re: Stret dvou objektu leticich po trajektorii

#15 28. 10. 2012 13:39

Re: Stret dvou objektu leticich po trajektorii

#16 28. 10. 2012 14:33 — Editoval liquid (28. 10. 2012 14:34)

Re: Stret dvou objektu leticich po trajektorii

#17 28. 10. 2012 15:50

Re: Stret dvou objektu leticich po trajektorii

#18 29. 10. 2012 13:43

Re: Stret dvou objektu leticich po trajektorii

#19 29. 10. 2012 20:13 — Editoval pietro (29. 10. 2012 21:07)

Re: Stret dvou objektu leticich po trajektorii

#20 29. 10. 2012 20:23

Re: Stret dvou objektu leticich po trajektorii

#21 29. 10. 2012 20:49

Re: Stret dvou objektu leticich po trajektorii

#22 29. 10. 2012 21:14

Re: Stret dvou objektu leticich po trajektorii

#23 29. 10. 2012 21:20

Re: Stret dvou objektu leticich po trajektorii

#24 29. 10. 2012 22:16

Re: Stret dvou objektu leticich po trajektorii

#25 29. 10. 2012 23:45

Re: Stret dvou objektu leticich po trajektorii

Zápatí