Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 11. 2008 19:26 — Editoval O.o (29. 11. 2008 19:27)
Integrace
Ahoj :),
rád bych Vás požádal o pomoc s integracemi.
Přesněji mám problém u dvou a to těchto:
Add 1) U téhle integrace mi už nějak došli nápady (zkouším tu integrovat ze sbírky matematiyk již asi čtyři hodiny, ale tady opravdu nevím, moc mi to holt nemyslí..).
- Zkoušel jsem to nějak upravit, abych tam mohl něco substituovat, ale stejně jsem vlastně nedošel k něčemu použitelnému do substituce.![kopírovat do textarea $ \int{\sqrt{\frac{1+\sqrt{x}}{\sqrt{x}}}}= \int{\frac{\sqrt{1+\sqrt{x}}}{\sqrt{\sqrt{x}}}}= \int{\frac{\sqrt{1+\sqrt{x}}}{x}}= \int{\frac{1}{x}\cdot \sqrt{1+\sqrt{x}}}= \int{\frac{1}{x}\cdot \sqrt{\sqrt{x}(\frac{1}{\sqrt{x}}+1)}}= \int{\frac{\sqrt[4]{x}}{x}\cdot \sqrt{(\frac{1}{\sqrt{x}}+1)}}= \int{\frac{1}{\sqrt[4]{x^3}}\cdot \sqrt{(\frac{1}{\sqrt{x}}+1)}}=X $](/mathtex/db/db1c05b58ac38cfa4d0d2e3ed63a3dec.gif)
- No co tu budu povídat, upravoval jsem to, jak mne jen napadlo, čistě mechanicky bez přemýšlení - tak nějak mi začínají ty integrace lézt postupně na nervy => chce to přestávku. Úprava byla celkově vzato na vě věci. Substituci jsem z toho žádnou nevykoukal.
- Napadá mne snad jedině, že by se něco do a před integraci přidalo? Kdyby se tam dal (před int. i do int.) přidat nějaký pěkný zlomek typu 1/x bylo by to skvělé, ale mám to tušení, že bych tím zbortil celou tu integraci (jednoduše, že to takto nepůjde).
Add 2) Jediné co vím je, že bych tam měl použít cos(x), ale nemám tušení jak a hlavně proč.
Byl by někdo, tak ochotný a neporadil by mi prosím s těmito příklady?
Děkuji předem za nakopnutí (nejlépe pořádné ;)), případně za krátké dovysvětlení.
Offline
#5 29. 11. 2008 19:50 — Editoval ttopi (29. 11. 2008 19:52)
Re: Integrace
Mě napadla ještě substituce  pak máme
pak máme 
Teď bych volil další substituci, zřejmě Eulerovu a mohlo by něco vyjít.
EDIT: Pak mi ale program opět nabízí substituci na sin(x) tak už nevím, jestli to jde bez toho, zřejmě tedy ne. :-)
oo^0 = 1
Offline
#6 29. 11. 2008 20:11 — Editoval Pavel (29. 11. 2008 20:30)
Re: Integrace
↑ ttopi:
ad 2) Ještě mě napadá metoda per partes. Ta by tady taky šla použít.
Pokud se na to podívám jako na rovnici s neznámou I, dostanu hned výsledek
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#7 29. 11. 2008 20:23
Re: Integrace
↑ ttopi:
No, mne by ani, tak nevadilo, že se tam mají našoupnout ty gon. funkce, jen vůbec netuším proč a díky tomu ani kdy..
Eulerova substituce mi, musím podotknout, nic neříká .). Vlastně mám to tušení, že jsme ji ve škole ani nezmiňovali .)
Offline
#8 29. 11. 2008 21:02 — Editoval kaja.marik (29. 11. 2008 21:08)
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Integrace
Jsou to standardni substituce x=a*sin(t) nebo a*cos(t)
x=a*sin(t) nebo a*cos(t) x=a*tan(t)
x=a*tan(t)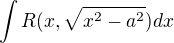 x=a/cos(t)
x=a/cos(t)
tyhle triky jsou naprosto obvyklé, jako třeba Kájův pozdrav :)
R(.,.) je racionální funkce dvou proměnných
--------------------------------------------------
Rozběhl se do lesovny. Po obvyklém druhém pozdravu spustil: „Vzácná paní, my půjdeme dnes na Dobříš se strejčkem Škrábkovic z Rochot. Tak bysme tam vzali třeba pár řádků panu řediteli. Maminka nám dá jídlo a pár korun. Zdeňa si musí pospíšit a vzít střevíčky s sebou. Ta bude koukat, jak rostou na stromě citrony zrovínka jako jablka. Ona beztoho myslí, že třeba ani nikde nerostou. Péťa půjde taky a váš Nero by mohl taky jít a že bysme si koupili ty hodně slané housky a u Šprunglů něco.“
Offline
#9 29. 11. 2008 23:04
#10 29. 11. 2008 23:42
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Integrace
krome toho x=a*tan(t) zabere jeste x=a*sinh(t) (hyperbolicky sinus nebo kosinus)
Offline
#11 30. 11. 2008 00:12 — Editoval O.o (30. 11. 2008 10:05)
Re: Integrace
↑ kaja.marik:
Ještě jednou ti děkuji. Zkusím zůstat u té tangenty, hyperbolický sinus je na mne v tuhle chvíli asi moc .)
EDIT: Koukal jsem se znovu do sbírky příkladů, protože mi stejně nedá, že nezvládám nějak vyřešit tu první integraci s odmocninou. Nakonec jsem zjistil, že se do zadání dostala chyba, ta odmocnina ve jmenovateli by být neměla (tzn. mělo by tam být pouze x) - tisková chyba, kdo ví? Dále už jsem schopný vyřešit tuto integraci i s pomocí valstních sil, ale čistě ze zvědavosti, dalo by se to nějak řešit s tou odmocninou?
Děkuji
Offline

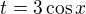 .
.