Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 11. 2012 14:41
zaujimava seria
Zda sa mi ze toto cvicenie je velmi zaujimave.
Vysetrite ci rada vseobecneho clenu:
je konverrgentna alebo divergentna?
Kto nam ho vyriesi?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 04. 11. 2012 15:37 — Editoval vanok (04. 11. 2012 15:38)
Re: zaujimava seria
Ahoj ↑ didik:,
Zial to nie je riesenie.
Hladaj este....
Ak treba dam nejaku pomoc.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 05. 11. 2012 16:18
Re: zaujimava seria
↑ vanok:
Bohužel je tato úloha neúplná. Míníme-li formální výraz
potom se nejedná o nekonečnou řadu reálných čísel. Je nutno specifikovat indexovou množinu, potom má smysl zabývat se úlohou seriózně. Důvodem není popichování účastníka fóra, ale mé poučení o tom, že změna indexové množiny nekonečné řady reálných čísel znamená někdy zásadní změny v konvergenci studované řady.
Offline
#6 05. 11. 2012 17:43 — Editoval vanok (05. 11. 2012 17:45)
Re: zaujimava seria
Pozdravy,
↑ Marian:
Podla mna, ak to nie je napisane, ide o radu uvazovanu na najvadcej moznej vhodnej podmnozine z 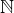 . Co da uz prvu uvahy o rade.
. Co da uz prvu uvahy o rade.
ako to poznamenal kolega ↑ Brano:
Inac, sa mi zda, ze ide o cvicenie, z ktoreho, zaciatocnik moze mat osoh.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 06. 11. 2012 12:33
Re: zaujimava seria
↑ vanok:
Hledal jsem nejelementárnější cestu. Řešení jsem již našel, teď si najít chvíli času a napsat to tady. Snad mi to vyjde ještě tento týden.
Případně se těším na řešení kolegů/kolegyň.
Offline
#8 06. 11. 2012 15:29
Re: zaujimava seria
↑ Marian:,
Ahoj, rad si precitam tvoj dokaz, moj spociva previest tuto radu na sucet troch konvergeentnych rad... Ak budem mat trochu casu, napisem ho tu.
I ked by som rad; videl nejake dokazy, od kolegov, co su este studenty.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 08. 11. 2012 13:05 — Editoval Marian (08. 11. 2012 13:30)
Re: zaujimava seria
Nabízím své elementární řešení...
EDIT
Jak jsem však právě našel, lze aplikovat i tzv. Dedekindovo kriterium konvrgence nekonečné řady (viz např. zde).
Offline
#10 08. 11. 2012 14:26 — Editoval vanok (13. 11. 2012 18:54)
Re: zaujimava seria
Pozdravujem ↑ Marian: a dakujem, ze ta tento maly problem zaujal, ako aj vsetkych inych, co skusili ho vyriesit,
Pridavam dalsie riesenie (neelementarne ale trochu kratcie).
Poznamky:
1°
2°
Edit: upresnenie jedneho pojmu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 08. 11. 2012 20:32 — Editoval check_drummer (10. 11. 2012 20:27)
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: zaujimava seria
Ahoj, zkusil jsem toto:
(Děkuji kolegovi vanok za upozornění na chybu. Opravil jsem. Naštěstí nemá podstatný vliv na výsledek.)
"Máte úhel beta." "No to nemám."
Offline
#12 09. 11. 2012 08:44
Re: zaujimava seria
↑ check_drummer:
U neabsolutně konvergentních řad nelze jednoduše skupinkovat.
Offline
#13 09. 11. 2012 20:56
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: zaujimava seria
↑ Marian:
Ahoj, existuje nějaký protipříklad? (Pozor, skupinkuji, avšak nepermutuji...)
Dle mého bude mít posloupnost částečných součtů po "skupinkování" stejnou limitu jako bez skupinkování, tj. označím-li např. pro obecnou  , kde
, kde 

a  pro n=2k-1 (pro n sudé bychom postupovali analogicky),
pro n=2k-1 (pro n sudé bychom postupovali analogicky), pak je
pak je  pro N sudé
pro N sudé pro N liché
pro N liché
Ovšem jelikož  , máme shodnou limitu pro S(N) a T(N)...
, máme shodnou limitu pro S(N) a T(N)...
Jinými slovy, z konvergence T(N) plyne konvergence S(N).
"Máte úhel beta." "No to nemám."
Offline
#14 11. 11. 2012 15:40 — Editoval vanok (11. 11. 2012 15:41)
Re: zaujimava seria
Ahoj e]p314926|check_drummer[/re],
Klasicky mame tuto radu:
1-1+1-1+1-1+...
A podla grupovania dostanes
(1-1)+(1-1)+... , cize 0+ 0 + 0 +...
alebo aj
1 +(-1+1) + (-1+1)+... , cize 1+0 + 0 +...
Preto, zda sa mi, kolegovu poznamku, mozes aj takto interpretovat. Aka vlasnost ti povoluje grupovat ( skupinkovat) jej cleny.
V literature o tom iste najdes. Ide tzv. processusy "sumacie". Ak ta to zaujima podrobnejsie, a nic nenajdes na webe, napis nam tu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 11. 11. 2012 21:19
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: zaujimava seria
↑ vanok:
Ano, ale naše řadá má podstatnou vlastnost - limita jejích členů jde k 0, tedy lze (dle mého) použít mou úvahu výše o ekvivalentním tvrezní o konvergenci obou řad.
"Máte úhel beta." "No to nemám."
Offline
#17 11. 11. 2012 23:20 — Editoval vanok (12. 11. 2012 15:41)
Re: zaujimava seria
Ahoj ↑ check_drummer:,
Najprv, pripominamù, ze som vobec nekontestoval tvoj vysledok, chcem ta len dovies k presnemu vyroku (VETE) co musi splnovat grupovanie radov, tak aby sa neznmenila jej konvegencia.
A teraz ti dam dalsi priklad na grupovanie?
Uvazujme toto grupovanie:
( ktora je striktne stupajuca  ) .
) .
Pre  ak
ak 
a  ak
ak  .
.
Polozme ![kopírovat do textarea $v_p= \sum_{n= \varphi(p)}^{\varphi (p+1]-1} u_n$](/mathtex/3f/3f1cc3020d121ba14f827998f4a1ca62.gif) .
.
Tu mame  .
.
A co mame pre 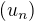 a pre
a pre  ?
?
odpoved
A teraz veta, co urci podmienky, kedy je mozne grupovanie ( pripade klasickych radov ... co je jednoduchy pripad "sumacie")
Veta:
Uvazujme rad
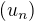 ( z clenmy v
( z clenmy v  )
)a
 , striktne stupajucu aplikaciu z
, striktne stupajucu aplikaciu z 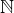 do
do 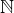 ; taku ze
; taku ze  .
.Definujme radu
 tak, ze
tak, ze ![kopírovat do textarea $v_p= \sum_{n= \varphi(p)}^{\varphi (p+1]-1} u_n$](/mathtex/3f/3f1cc3020d121ba14f827998f4a1ca62.gif) .
.Ak postupnost
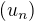 konverguje k
konverguje k 
a
ak
 je konecna ( bornée).
je konecna ( bornée).Vtedy konvergencia rady
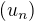 je ekvivalentna z kovergenciou rady
je ekvivalentna z kovergenciou rady 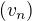 .
.( a vtedy maju tu istu limitu )
Poznamka:
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#18 13. 11. 2012 17:44
Re: zaujimava seria
↑ check_drummer:
Ahoj, nemohl jsem se dostat dříve ke zdejšímu fóru. Máš naprostou pravdu. Lze vyštřit konvergenci tebou navrženým způsobem. Podstatné je, že posloupnost {a_n} je nulová, tj. má nulovou limitu.
Nevím, proč mě to nenapadlo, řešit úlohu tímto způsobem.
Offline
#19 13. 11. 2012 18:39
Re: zaujimava seria
↑ Honza90:
Ano alternuje, tipol by som ze vanok tym myslel, ze nesplna kriterium pre konvergenciu alternujuceho radu. (Leibnizovo sa tusim vola.)
Offline
#20 13. 11. 2012 18:52 — Editoval vanok (13. 11. 2012 23:20)
Re: zaujimava seria
↑ Brano:, Presne ako pises, chcel som vyjadrit, ze ta rada nesplna hypotezy vety o alternujucom rade: cize neustale meni znamienko a aj v absolutnej hodnote klesa k nule.
( reeditujem to vyssie, aby to nebolo nepresne)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

 . Řada s takovýmto n-tým členem diverguje, protože n-tý člen nejde k nule, a tedy i původní řada musí divergovat.
. Řada s takovýmto n-tým členem diverguje, protože n-tý člen nejde k nule, a tedy i původní řada musí divergovat. nema zmysel, tak predpokladam, ze sa jedna o rad
nema zmysel, tak predpokladam, ze sa jedna o rad  takto:
takto: , kde
, kde předpisem
předpisem -tý parciální součet předložené nekonečné řady do tvaru
-tý parciální součet předložené nekonečné řady do tvaru závěr
závěr máme celkem pro původní nekonečnou řadu
máme celkem pro původní nekonečnou řadu mame
mame
 tato metoda by nefungovala; ak niekto chce nech to skusi... a tiez nech skusi najst jedno resenie.
tato metoda by nefungovala; ak niekto chce nech to skusi... a tiez nech skusi najst jedno resenie.
 .
. nie su potrebne, ale vo vseobecnom pripade ANO
nie su potrebne, ale vo vseobecnom pripade ANO , takže zřejmě
, takže zřejmě  .
.  dostáváme
dostáváme ,
,  a kvůli druhé z těchto nerovností nelze aplikovat Leibnizovo kriterium.
a kvůli druhé z těchto nerovností nelze aplikovat Leibnizovo kriterium. 
 a dále
a dále  .
.  , což ze vztahů (2) snadno ověříme zvlášť pro
, což ze vztahů (2) snadno ověříme zvlášť pro  (k součtu 0) je s ohledem na definici posloupnosti
(k součtu 0) je s ohledem na definici posloupnosti  a (0) triviální.
a (0) triviální.  zřejmě stačí dokázat konvergenci řady
zřejmě stačí dokázat konvergenci řady 
 ,
,  ,
,  je konvergentní,
je konvergentní,