Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 11. 2012 21:04 — Editoval JohnPeca18 (05. 11. 2012 21:04)
- JohnPeca18

- Příspěvky: 651
- Škola: MFF UK
- Pozice: Absolvent 2014
- Reputace: 81
Limita
Potrebujem spocitat limitu, teda viem vysledok ale neviem ako sa k nemu dostat.
http://www.wolframalpha.com/input/?i=%2 … o+infinity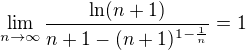
Napada vas neco?
Offline
- (téma jako vyřešené označil(a) JohnPeca18)
#3 05. 11. 2012 22:14
- JohnPeca18

- Příspěvky: 651
- Škola: MFF UK
- Pozice: Absolvent 2014
- Reputace: 81
Re: Limita
↑ Brano:
Diky, nerozumiem celkom ale ako tam napasovat tu substituciu, ako si vyjadrim n?
Offline
#4 05. 11. 2012 23:56
Re: Limita
↑ JohnPeca18:
Pravda, takto to vidiet dost tazko. Ja som najprv urobil  upravil a potom
upravil a potom 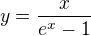 , len tam ostalo
, len tam ostalo 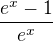 , ale to je 1.
, ale to je 1.
Offline
#5 07. 11. 2012 14:38 — Editoval JohnPeca18 (07. 11. 2012 14:45)
- JohnPeca18

- Příspěvky: 651
- Škola: MFF UK
- Pozice: Absolvent 2014
- Reputace: 81
Re: Limita
↑ Brano:
Tak vratil som sa k tomuto prikladu, poprosil by som o skontrolovanie.
Moze to byt takto?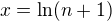
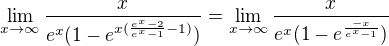
Potom pre 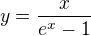
to je
Offline
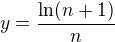 . Az na nejaky faktor
. Az na nejaky faktor 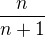 to pekne prejde na
to pekne prejde na 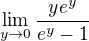 a potom L'Hopital a je hotovo.
a potom L'Hopital a je hotovo.