Matematické Fórum

mb305 · 08. 11. 2012 05:44

Dobré ráno,

chtěl bych se vás zeptat, zda má úvaha je správná.

Hledám obor hodnot pro funkci: 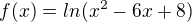$f(x) = ln(x^2 - 6x + 8)$ . Definiční obor mám 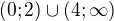$(0; 2) \cup (4; \infty)$ . Vzhledem k tomu, že maximum kvadratické funkce 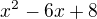$x^2 - 6x + 8$ není definované (tedy fnkce má pouze minimum a na intervalu 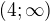$(4; \infty)$ roste až k $\infty$ ), tak předpokládám, že obor hodnot je celé R.

JohnPeca18 · 08. 11. 2012 10:03

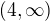Kedze je funkce na $(0,2)$ spojita a klesajici a na $(4,\infty)$ spojita a stoupajici, tak obor hodnot bude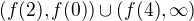 $(f(2),f(0))\cup (f(4),\infty)$
To ze stoupa do nekonecna to jo. Ale je to omezeny z dola.

mb305 · 09. 11. 2012 16:07

Díky moc :-)

Matematické Fórum

#1 08. 11. 2012 05:44

Logaritmická funkce, hf

#2 08. 11. 2012 10:03

Re: Logaritmická funkce, hf

#3 09. 11. 2012 16:07

Re: Logaritmická funkce, hf

Zápatí