Matematické Fórum

Bugwin · 13. 11. 2012 22:20

dobry vecer,

mam takovy problem, resim jednu rovnici

$4\sqrt{x+6}=x+1$ odmocnil jsem to nadruhou, a vyslo mi

$16x+6=x^{2}+2x+1$ Upravim to a vyjde mi .

$14x+5-x^{2}=0$ Ted musim vypocitat $x_{1} x_{2}$

Pomoci $x_{1,2}=\frac{-b\pm \sqrt{b^{2}-4\cdot ac}}{2\cdot a}$

Vyjde mi $x_{1,2}=\frac{-5\pm \sqrt{5^{2}-4\cdot 14x\cdot x^{2}}}{2\cdot a}$

A tady jsem skoncil protoze nevim jak to vypocitat, asi proto ze jsem nedaval pozor .
Nevim jak mam vynasobit mezi sebou to $a\cdot c$

Doufam ze jsem to aspon pocital spravne , a budu moc vdecny jestli mi poradite.
Dekuji moc

Mr.Pinker · 13. 11. 2012 22:24

už druhej řádek máš špatně .... mimochodem do diskriminantu se dosazují jen koeficienty z toho polynomu

mikl3 · 13. 11. 2012 22:36 — Editoval mikl3 (13. 11. 2012 22:37)

Bugwin napsal(a):
odmocnil jsem to nadruhou

zajímavá úprava :)

Bugwin · 13. 11. 2012 22:36

Ach, to je fakt pekny, proste mi to nejde :(

mikl3 · 13. 11. 2012 22:38

↑ Bugwin: umocnil jsi $$4\sqrt{x+6}$^2=16(x+6)$

Bugwin · 13. 11. 2012 22:44 — Editoval Bugwin (13. 11. 2012 22:48)

No ve skole nam dnes rikali ze $x+1 =>>$ (A\pm B)^{2} = A^{2}\pm 2AB+B^{2}
tak jsem to delal podle toho.

mikl3 · 13. 11. 2012 22:45

↑ Bugwin: to je správně a platí to pro pravou stranu, ale já mluvil o levé $$4\sqrt{x+6}$^2=16(x+6)$

Bugwin · 13. 11. 2012 22:47

No vsak $\sqrt{}$ zmizi a 4 se vynasobi 4rkou, to je spravne ne?

mikl3 · 13. 11. 2012 22:49

↑ Bugwin: ano, ale ty jsi do úpravy rovnice napsal, že $$4\sqrt{x+6}$^2=16x+6$ což se nerovná

Bugwin · 13. 11. 2012 22:51

mikl3 napsal(a):
↑ Bugwin: ano, ale ty jsi do úpravy rovnice napsal, že $$4\sqrt{x+6}$^2=16x+6$ což se nerovná

takze to je $16x+24$ ?

mikl3 · 13. 11. 2012 22:52

↑ Bugwin: $16x+16\cdot 6$

mikl3 · 13. 11. 2012 22:53

$$4\sqrt{x+6}$^2=16(x+6)$ neboli toto

Bugwin · 13. 11. 2012 22:55

Aha takze to bude

$16x+96=x^{2}+2x+1$ ?

mikl3 · 13. 11. 2012 22:56

↑ Bugwin: ano

Bugwin · 13. 11. 2012 23:00

Ted mi to vyslo :

$x_{1,2}=\frac{-96\pm \sqrt{9216-4\cdot 16x\cdot x^{2}}}{192}$

Ted jsem u stejnyho problemu na ktery jsem se ptal, jak vynasobim to $16x\cdot x^{2}$ ?

mikl3 · 13. 11. 2012 23:02 — Editoval mikl3 (13. 11. 2012 23:04)

↑ Bugwin: zase se odvolám na nápovědu od ↑ Mr.Pinker: a to sice, že do rovnice pro výpočet kořenů kv. rovnice dosazuješ koeficienty $a,b,c$ z $ax^2+bx+c=0$
ty jsi tam dosadil i x, to by tam být nemělo, dokážeš předělat?
nekontroluji čísla, ale také doporučuji napsat rovnici do tvaru $x^2-14x-95=0$

Bugwin · 13. 11. 2012 23:10 — Editoval Bugwin (13. 11. 2012 23:15)

Jej ja jsem tu rovnici jeste ani neupravil.

$14x+95-x^{2}=0$

Takze to bude :

$x_{1,2}=\frac{-14\pm \sqrt{196-4\cdot 1\cdot 95}}{28}$

Ze?

Aha takze

mikl3 · 13. 11. 2012 23:13

↑ Bugwin: nemusíš ji upravovat, je správně, ale já jsem to napsal proto, protože se ti to plete
koeficienty 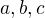$a, b, c$ bys měl čerpat z přepsaného tvaru $x^2-14x-95=0$
protože $a$ je koeficient u členu kvadratického, $b$ u lineárního a $c$ je člen absolutní
ale tys to pomíchal, protože sis myslel, že "prostřední člen" tedy $b$ ve tvé rovnici $14x+95-x^{2}=0$ je $95$
ale je to $14$
rozumíš?

Bugwin · 13. 11. 2012 23:19 — Editoval Bugwin (13. 11. 2012 23:28)

Ja to chapu , jen se mi to porad plete, doufam ze ted je to spraven:

$x_{1,2}=\frac{14\pm \sqrt{196-4\cdot 1\cdot (-95)}}{2}$

mikl3 · 13. 11. 2012 23:20 — Editoval mikl3 (13. 11. 2012 23:21)

↑ Bugwin: až na znaménko u $c$ správně, stačí dopočítat a provést zkoušku, protože ta úprava umocnění nebyla zase až tak ekvivalentní

Bugwin · 13. 11. 2012 23:23 — Editoval Bugwin (13. 11. 2012 23:27)

takze je to $\frac{14\pm \sqrt{576}}{2}$

mikl3 · 13. 11. 2012 23:24

↑ Bugwin: koukám, že načítáš stránky velice rychle, já jsem ten příspěvek po kontrole změnil :)

Bugwin · 13. 11. 2012 23:28

Me jenom rve program ze prisel novy email :) Taky jsem to upravil , doufam ze spravne

mikl3 · 13. 11. 2012 23:28

↑ Bugwin: taky edituješ, a to do správné podoby
vypočítat ty kořeny a provést zkoušku

mikl3 · 13. 11. 2012 23:29 — Editoval mikl3 (13. 11. 2012 23:32)

↑ Bugwin: aha, z odběru příspěvků ze svého tématu (což je automaticky nastavené) se můžeš odhlásit, ale to je jedno

téma jsme úspěšně skorovyřešili, teď už je to na tobě, já totiž jdu spát, kdyby něco, ráno se na to kouknu, nebo někdo jiný odpoví

Matematické Fórum

#1 13. 11. 2012 22:20

Iracionalni rovnice

#2 13. 11. 2012 22:24

Re: Iracionalni rovnice

#3 13. 11. 2012 22:36 — Editoval mikl3 (13. 11. 2012 22:37)

Re: Iracionalni rovnice

Bugwin napsal(a):

#4 13. 11. 2012 22:36

Re: Iracionalni rovnice

#5 13. 11. 2012 22:38

Re: Iracionalni rovnice

#6 13. 11. 2012 22:44 — Editoval Bugwin (13. 11. 2012 22:48)

Re: Iracionalni rovnice

#7 13. 11. 2012 22:45

Re: Iracionalni rovnice

#8 13. 11. 2012 22:47

Re: Iracionalni rovnice

#9 13. 11. 2012 22:49

Re: Iracionalni rovnice

#10 13. 11. 2012 22:51

Re: Iracionalni rovnice

mikl3 napsal(a):

#11 13. 11. 2012 22:52

Re: Iracionalni rovnice

#12 13. 11. 2012 22:53

Re: Iracionalni rovnice

#13 13. 11. 2012 22:55

Re: Iracionalni rovnice

#14 13. 11. 2012 22:56

Re: Iracionalni rovnice

#15 13. 11. 2012 23:00

Re: Iracionalni rovnice

#16 13. 11. 2012 23:02 — Editoval mikl3 (13. 11. 2012 23:04)

Re: Iracionalni rovnice

#17 13. 11. 2012 23:10 — Editoval Bugwin (13. 11. 2012 23:15)

Re: Iracionalni rovnice

#18 13. 11. 2012 23:13

Re: Iracionalni rovnice

#19 13. 11. 2012 23:19 — Editoval Bugwin (13. 11. 2012 23:28)

Re: Iracionalni rovnice

#20 13. 11. 2012 23:20 — Editoval mikl3 (13. 11. 2012 23:21)

Re: Iracionalni rovnice

#21 13. 11. 2012 23:23 — Editoval Bugwin (13. 11. 2012 23:27)

Re: Iracionalni rovnice

#22 13. 11. 2012 23:24

Re: Iracionalni rovnice

#23 13. 11. 2012 23:28

Re: Iracionalni rovnice

#24 13. 11. 2012 23:28

Re: Iracionalni rovnice

#25 13. 11. 2012 23:29 — Editoval mikl3 (13. 11. 2012 23:32)

Re: Iracionalni rovnice

Zápatí