Matematické Fórum

Dobrý večer,
   Môj problém vedie na úlohu



Snažím sa reprodukovať výsledky pre lin. stabilitnú teóriu Orr-Sommerfeld systémov - stabilita Poiseuilleho toku (liter.: Drazin). Ide o problém 4. rádu, ktorý po aplikácií Čebyševovej diskretizácie možno zapísať v uvedenom tvare. Čebyševovské matice konštruujem podľa liter.: Trefethen: Spectral method in Matlab. Tieto sú vo všeobecnosti zle podmienené, najmä vo vyšších rádoch. Z matlabu potrebujem vydolovať nie len štruktúru spektra ale aj štruktúru vlastných vektorov .
    Mojim problémom je citlivosť vzhľadom na počet diskretizačných uzlov v prípade vlastných vektorov. Normálne by som očakával konvergenciu k statickému riešeniu po zjemnení, avšak toto sa nedeje. Naopak v prípade spektra, toto zostáva správne. Čo môže byť príčinou, že vlastné číslo je spočítané presne a prislúchajúci vlastný vektor sa mení v závislosti od jemnosti diskretizácie?

Vlastný vektor v mojom prípade reprezentuje diskrétnu aproximáciu vlastnej funkcie. Podobné problémy som nepostrehol pri riešení problému 2. rádu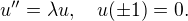

V tom prípade sú vlastné čísla ako aj prislúchajúce vlastné vektory spočítané správne a konvergujú k teoretickým.

Ak sa niekto s niečím podobným stretol, budem vďačný za pomoc..