Matematické Fórum

Dale.Lenka · 25. 11. 2012 18:51

Ahoj, doučuju jednoho známého. Dnes za mnou přišel s rozklady na součin. Drtivou většinu jsem zvládla, ale u tohodle příkladu si nejsem jistá, jestli by stačilo takové řešení. Víc mě totiž nenapadá.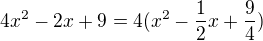

$4x^{2}-2x+9 = 4(x^{2}-\frac{1}{2}x+ \frac{9}{4})$

Jde to rozložit ještě nějak víc?

A ještě bych poprosila o kontrolu tohoto příkladu: $(a^{5}-1)=(a-1)[a(a+1)(a^{2}+1)+1]$

Díky za radu, Lenka

((:-)) · 25. 11. 2012 18:55 — Editoval ((:-)) (25. 11. 2012 19:04)

↑ Dale.Lenka:

Rozkladať sa dá rôzne, ten trojčlen v zátvorke sa už "klasicky" rozložiť nedá, ale to asi vieš.

Autor skryl část textu. Zobrazit/skrýt!

Druhý príklad - je to ono, ale načo je vnútri zátvorky ten súčin ?

nejsem_tonda · 26. 11. 2012 07:55

↑ ((:-)):
"Neklasicky" (v oboru komplexnich polynomu) se to rozlozit da. Treba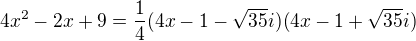
$4x^2-2x+9=\frac14(4x-1-\sqrt{35}i)(4x-1+\sqrt{35}i)$ .
Samotne vytknuti ctyrky se obvykle za rozklad nepovazuje (to bych si mohl vytknou jakekoliv cislo).

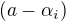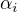Druhy priklad je soucin peti zavorek typu $(a-\alpha_i)$ , kde $\alpha_i$ jsou komplexni pate odmocniny z jednicky.

((:-)) · 26. 11. 2012 09:48 — Editoval ((:-)) (26. 11. 2012 18:21)

↑ nejsem_tonda:

:-)

Samozrejme, máš pravdu (aj keď podľa mňa aj vyňatie čohokoľvek okrem 0 je tiež rozklad na súčin - zober si, že sa potom dá vo výraze krátiť číslom alebo premennou...) .

Mala som napísať, že v R (ale možno sa o C ešte neučili, potom sa R berie ako samozrejmosť).

Tipujem, že ak by hľadali rozklady nad C, tak by si to naša zadávateľka uvedomila a nedávala by sem post, ale môžem sa mýliť ...

Dale.Lenka · 26. 11. 2012 18:16

↑ ((:-)):↑ ((:-)):

Vzhledem k tomu, že se jedná o klučinu v prvním ročníku střední školy, tak tyto příklady opravdu řeší pouze v oboru reálných čísel. Díky moc za všechny reakce :-)

BakyX · 26. 11. 2012 18:25 — Editoval BakyX (26. 11. 2012 18:27)

↑ Dale.Lenka:

$a^5-1$ sa dá v $\mathh{R}$ ešte dá ďalej rozkladať:

$a^5-1=$a-1$$a^2-\frac{a(\sqrt{5}-1)}{2}+1$$a^2+\frac{a(\sqrt{5}+1)}{2}+1$$

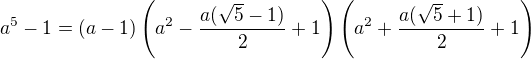
Prísť na to však vyžaduje zložitejšiu teóriu a asi sa neočakáva, že na to žiak 1. ročníka príde.

Matematické Fórum

#1 25. 11. 2012 18:51

Rozklad na součin

#2 25. 11. 2012 18:55 — Editoval ((:-)) (25. 11. 2012 19:04)

Re: Rozklad na součin

#3 26. 11. 2012 07:55

Re: Rozklad na součin

#4 26. 11. 2012 09:48 — Editoval ((:-)) (26. 11. 2012 18:21)

Re: Rozklad na součin

#5 26. 11. 2012 18:16

Re: Rozklad na součin

#6 26. 11. 2012 18:25 — Editoval BakyX (26. 11. 2012 18:27)

Re: Rozklad na součin

Zápatí