Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 11. 2012 18:48
Zápis množiny
Dobrý den, potřebuji pomoci v problematice množin.
Mám množinu racionálích prvků x. Prvky x, kterých je nekonečně mnoho patří do množiny A. Jaký je správný zápis množiny, pokud pro prvky x platí předpis : x= p/3^q; p,q je prvkem celých čísel.
Děkuji za odpovědi.
peetr1
Offline
#2 28. 11. 2012 21:34 — Editoval peetr1 (28. 11. 2012 21:40)
Re: Zápis množiny
↑ peetr1:
Dobrý večer ještě jednou.
Zatím žádná reakce, takže se pokusím moji problematiku více rozvinout. Mám dilema, jestli to, co jsem výše popsal není vlastně funkce x= p/3^q,kde p,q je prvkem množiny všech celých čísel Z. Potom obor hodnot funkce f(x), by byly vlastně prvky množiny A.
Jenže tento obor hodnot funkce (nebo množina A ?) je mým novým definičním oborem, který potřebuji doplnit do jiné funkce.
Nevím kde je hranice, co vlastně považujeme za množinu a co už je funkce. Omlouvám se za možná primitivní otázky, ale nějak se v této problematice ztrácím.
Děkuji za Vaše názory, případně odkazy.
Peetr1
Offline
#3 28. 11. 2012 22:21 — Editoval peetr1 (28. 11. 2012 22:25)
Re: Zápis množiny
↑ ((:-)):
Děkuji za reakci,
tak nějak jsem si to představoval, jenom si myslím, že by měla být uvedena množina i pro x.V zadání jsem dodatečně opravil : q je prvkem množiny N, tedy přirozených čísel.
Můžete ještě někdo posoudit prosím správnost zápisu?
Dík .
Offline
#4 29. 11. 2012 07:26
Re: Zápis množiny
↑ peetr1:
to  tam být nemusí, je to jasné z definice čísel
tam být nemusí, je to jasné z definice čísel 
jinak ustálené číselné množiny je obvyklé psát dvojitě tažené
já bych to zapsal následovně
k tvému zápisu
- kdyby bylo  , nedostal bys racionální číslo 0
, nedostal bys racionální číslo 0
- kdyby bylo pouze  nedostaneš racionální čísla typu
nedostaneš racionální čísla typu 
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#5 29. 11. 2012 15:04
Re: Zápis množiny
Dobrý den,
@byk7 - dík za reakci. Snažil jsem se dopátrat co je ustálená číselná množina, nepodařilo se mě význam vyguglit. Vím, že to přímo nesouvisí s tématem,ale uvítal bych odkaz a bližší nasměrování.
Jinak k samotné definici množiny A.
- záměrem je, aby bylo 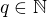 .
.
- záměrem je, aby 
Tato množina A bude následně definičním oborem jiné funkce, pro  a x=0 není tato funkce definována.
a x=0 není tato funkce definována.
Offline
#6 30. 11. 2012 00:01
Re: Zápis množiny
↑ peetr1:
hmm.., "ustálená číselná množina" je můj vlastní výraz
myslel jsem tím množiny čísel: přirozených, celých, racionálních, reálných, komplexních
místo  se používá spíš
se používá spíš 
dle tvojí námitky, bych množinu  potom zapsal jako
potom zapsal jako
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#7 30. 11. 2012 00:25
- Jirik-1357

- Příspěvky: 30
- Pozice: pracující
- Reputace: 0
Re: Zápis množiny
a protoze to zmate :) tak pripominam vsem, co to nevi, ze rozdil mnozin se zapisuje lomitkem :)
R - {0} = R\{0}
kde zapis s lomitkem je ten spravny byt oboji se pouzivalo (na strednich skolach)
Offline
#8 30. 11. 2012 01:50
#9 30. 11. 2012 06:52
- Jirik-1357

- Příspěvky: 30
- Pozice: pracující
- Reputace: 0
Re: Zápis množiny
↑ Mr.Pinker:
ne ze ma prednost, ale pokud jsem spravne poslouchal na hodinach matematiky (priznavam, ze toto uz bylo pred mnoha lety), je to primo formalni zapis pro mnozinovou matematiku. Z cehoz lze dle meho usuzovat, ze jde o zapis "spravnejsi" nikoli jediny spravny.
Ale to uz je jen formalni vyjadreni stejne jako psani 
PS za hadku me toto nestoji a o prednosti tu nebyla rec (uz vubec ne o prednosti v logice ci matematickem vypoctu)
Offline
#10 30. 11. 2012 17:41
Re: Zápis množiny
@All
Děkuji za reakce, hodně mě to pomohlo. Jinak ve wikipedii jsem se dočetl, že rozdíl množin je možné zapsat oběma způsoby. Tedy lomítkem i mínusem.
@byk7 ustálené množiny- rozumím tomu tak, že se jedná o kompletní množinu v níž nechybí žádný z prvků do dané množiny náležející.
Dík všem za pomoc a přeji příjemný wekend.
Offline
#11 30. 11. 2012 17:50
Re: Zápis množiny
↑ byk7:
Mal by som otázku. Považuje sa ten zápis za korektný z hľadiska toho, že zahrňuje nejaký prvkov viackrát ?
Napríklad pre 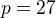 ,
, 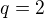 dostaneme rovnaký prvok ako pre
dostaneme rovnaký prvok ako pre 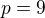 ,
, 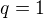 .
.
1^6 - 2^6 + 3^6 = 666
Offline
#12 30. 11. 2012 18:44
Re: Zápis množiny
Ahoj ↑ BakyX:,
V mnozinovom vyjadreni nevadi ak nejaky prvok je napisany viac krat, preto napr piseme  take, ze
take, ze 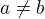 , ak chceme zarucit, ze ta mnozina ma 2 prvky.
, ak chceme zarucit, ze ta mnozina ma 2 prvky.
Ak by islo o postupnost tak by to zaviselo......
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 30. 11. 2012 18:45 — Editoval peetr1 (30. 11. 2012 18:54)
Re: Zápis množiny
@BakyX
Jsem přesvědčen o tom, že ano, jde o korektní zápis. Jde o množinu racionálních čísel, tzn.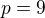
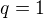 je vyjádřením racionálního čísla v základním tvaru ( vlastně bylo by to pro
je vyjádřením racionálního čísla v základním tvaru ( vlastně bylo by to pro 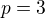
 - tzv nesoudělná čísla). Mrkni na obor racionálních čísel.
- tzv nesoudělná čísla). Mrkni na obor racionálních čísel.
Offline