Matematické Fórum

Skumin · 29. 11. 2012 20:33

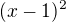Ahoj, zasekl jsem se uprostřed řešení této limity funkce: $\lim_{x\to1}\frac{x^{x-1}+\sqrt[3]{\cos \pi x}}{\log^{2}x}$ a potřeboval bych poradit, jak dál. Postupoval jsem takto: čitatel i jmenovatel jsem vynásobil výrazem $(x-1)^2$ , abych se zbavil logaritmu ve jmenovateli. Zbylo mi $1*\lim_{x\to1}\frac{x^{x-1}+\sqrt[3]{\cos \pi x}}{(x-1)^2}$ a teď nevím, jak dál. Chtěl bych použít známou limitu $\frac{\mathrm{e}^{x}-1}{x}$ , která je ve zlomku dobře vidět, pokud bych si výraz $x^{x-1}$ převedl na $\mathrm{e}^{(x-1)*\log{x}}$ , a pak čitatel i jmenovatel vynásobil výrazem $\log{x}$ . Ta známá limita by se tam podle mě poté dala použít, jenomže místo $-1$ tam mám $\sqrt[3]{\cos \pi x}$ , když tam ale dosadím $1$ , tak tu $-1$ tam jako by dostanu. Nicméně to pravděpodobně není korektní řešení. Věděl byste někdo, jak na to?

Mr.Pinker

$\lim_{x\to1}\frac{x^{x-1}+\sqrt[3]{\cos \pi x}}{\log^{2}x}=\lim_{x\to1}\frac{x^{x-1}-1}{\log^{2}x}+\lim_{x\to1}\frac{1+\sqrt[3]{\cos \pi x}}{\log^{2}x}$ s tímto bych začal respektive pro názornost bych si asi zavedl lineární substituci x=1+y

Skumin · 29. 11. 2012 22:02

Dobře, díky, kouknu na to :)

Matematické Fórum

#1 29. 11. 2012 20:33

Limita funkce

#2 29. 11. 2012 21:49 — Editoval Mr.Pinker (29. 11. 2012 21:50)

Re: Limita funkce

#3 29. 11. 2012 22:02

Re: Limita funkce

Zápatí