Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 02. 12. 2012 22:19
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Sinusova a kosinusova veta
↑ Qwerty0: Obsah trojuholníka sa dá vypočítať aj pomocou uhlov :  .
.
Offline
#5 03. 12. 2012 22:21
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Sinusova a kosinusova veta
↑ Qwerty0: Sú to 2 rovnice od 2 neznámych... uhol  si stačí dopočítať, neznáme sú strany a, b.
si stačí dopočítať, neznáme sú strany a, b.
Offline

 obsah,tak takto:
obsah,tak takto: (ak ten vzťah nepoznáš, môžem poslať návod na dôkaz)
(ak ten vzťah nepoznáš, môžem poslať návod na dôkaz)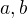 . Druhá vyplýva zo sínusovej vety:
. Druhá vyplýva zo sínusovej vety: