Matematické Fórum

Dworzaaa

Ahoj, zkousim odhad slozitosti pro: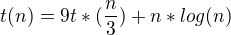
$t(n)=9t*(\frac{n}{3}) + n*log(n)$

Kdyz to zkousim pomoci mastertheoremu, tak mi vyjde:
$a=9 \ ,b=3 \ \log_{3}9=2\ \Rightarrow n*log(n)=O(n^{2-\varepsilon })$

tim padem: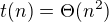
$t(n)=\Theta (n^{2})$

jenze iteracni metodou mi to nejak nevychazi...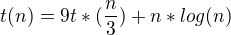
$t(n)=9t*(\frac{n}{3}) + n*log(n)$
$t(\frac{n}{3})=9t*(\frac{n}{9}) + \frac{n*log(n)}{3}$
$t(n)=9*(9t*(\frac{n}{9}) + \frac{n*log(n)}{3}) + n*log(n)$
$t(\frac{n}{9})=9t*(\frac{n}{27}) + \frac{n*log(n)}{9}$
$t(n)=729t*(\frac{n}{27}) +9*n*log(n) + 3*n**log(n) + n*log(n)$

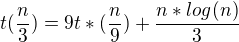
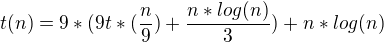
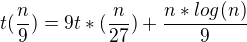
Jenze ted nevim uz moc, jak sestrojit tu sumu...
Vymyslel sem neco jako:
$n*(\small\sum\nolimits_{i=0}^{\log{3}{n}} (3^i) )$

ale tohle mi stezi da 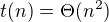$t(n)=\Theta (n^2)$ kte kterymu sem dosel za pomoci Master Theoremu... nemate nekdo nejakej tip, v cem by mohl bejt zakopanej pes?

Matematické Fórum

#1 04. 12. 2012 23:30 — Editoval Dworzaaa (08. 12. 2012 18:53)

Odhad slozitosti, iteracni metoda