Matematické Fórum

Milan1236000 · 07. 12. 2012 17:32

Zdravím, o elektrotechnice jsme začali počítat rezistory pomocí Kirchhoffových zákonů a počítáme to pomocí rovnic buď o 3 nebo 4 neznámých. O 3 to takš takš zvládám, ale o 4 mi to nějak nejde. Pomůžete mi prosím?

$I_{1} - I_{2} + I_{3} - I_{4} = 0$
$3I_{1} + 6I_{2} = 12$
$- 6I_{2} - 3I_{3} = - 12$
$3 I_{3} + 10 I_{4} = 3$

Díky.

Blackflower · 07. 12. 2012 18:15

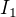↑ Milan1236000: Keďže je sústava lineárna, nenastane problém s nejakými šialenými zlomkami a podobne. Skús si napríklad z 3. rovnice vyjadriť $I_3$ , z druhej napríklad $I_1$ a dosadiť do zvyšných dvoch rovníc. Vyjde ti sústava rovníc o dvoch neznámych.

Milan1236000 · 07. 12. 2012 19:45

↑ Blackflower: Vyšlo mi, že $3I_{1}=I_{3}$ tak jsem pak zkusil spočítat podobným způsobem 3. a 4. rovnici a vyšlo mi $10I_{4}-6I_{2}=-9$ pak jsem tyhle dvě sečetl a dostal jsem tohle
$I_{1}-I_{2}+I_{3}-I_{4}=0$
$3I_{1}-6I_{2}-I_{3}+10I_{4}=-9$
Postupně jsem je zjednodušoval a dopracovával se k jednotlivým $I$ a vyšlo mi
$I_{1}=\frac{27}{32}$ $I_{2}=\frac{9}{32}$ $I_{3}=\frac{81}{32}$ $I_{4}=-\frac{9}{16}$ ale když jsem dosadil do rovnice $I_{1}-I_{2}+I_{3}-I_{4}=0$ tak to nevychází, nevím kde jsem udělal chybu.

Blackflower · 07. 12. 2012 20:55

↑ Milan1236000: Mne vyšlo $I_1=I_3$ , asi si sa niekde sekol v znamienku. Ešte na začiatku by bolo možno fajn predeliť 2. a 3. rovnicu trojkou, aby sa výpočty trošku zjednodušili.

Milan1236000 · 07. 12. 2012 22:11

↑ Blackflower: Máš pravdu, počítal jsem to znovu a zapoměl jsem tam něco, ale už mi to taky tak vyšlo. Ale štve mě že
$I_{1}-I_{2}+I_{3}-I_{4}=0$
$I_{1}-6I_{2}-I_{3}+10I_{4}=-9$
mi taky vychází že $I=-\frac{9}{16}$ takže stejně jako předtím až na ten malej rozdíl že předtím jsem tam měl
$I_{1}-I_{2}+I_{3}-I_{4}=0$
$3I_{1}-6I_{2}-I_{3}+10I_{4}=-9$
Já už fakt nevím... Nechápu co pořád dělám špatně že mi to nechce vycházet.

Blackflower · 07. 12. 2012 22:29

↑ Milan1236000: Môj postup:
Vyjadrenie 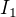$I_1$ a $I_3$ pomocou $I_2$ . Vychádza rovnaký výraz ( $4-2I_2$ ).
Dosadenie vyjadrených premenných do 1. a 4. rovnice - vychádzajú 2 rovnice o dvoch neznámych:
$8-5I_2=I_4$
$9-6I_2=-10I_4$
Vynásobila som prvú rovnicu 10 a pekne sa to odčítalo. Potom už len dorátať.
Riešenia, ktoré mi vypľul aj Microsoft Mathematics:
$I_1=I_3=\frac{23}{28}$
$I_2=\frac{89}{56}$
$I_4=\frac{3}{56}$