Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 08. 12. 2008 14:37
cauchyova uloha
Pomůže mi někdo s tímto příkladem?
Mám vypočítat deset takovýchto příkladů, ale jsou všechny podobné.
Stačí mi pomoct s jedním a já to pak už nějak spáchám. Jde mi hlavně o to jak udělat tu transformaci, dál už bych snad měl vědět, jak se počítá cauchyova úloha.
pomocí laplaceovy transformace najdi řešení cauchyovy ulohy
x'' + 4x = 2 cos(^2) * t
x(0) = 0
x'(0) = 0
Offline
#2 15. 11. 2009 15:56
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: cauchyova uloha
Podle tabulky (http://en.wikipedia.org/wiki/Laplace_tr … d_theorems) levou stranu:
a pravou stranu:
Vyjádříme  :
:
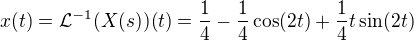
Offline