Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 11. 12. 2012 19:33

Dale.Lenka
Příspěvky: 70
Reputace:   0 
 

Integrál

Ahoj, potřebovala bych pomoct s integrálem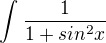

$\int_{}^{}\frac{1}{1+sin^{2}x}$

nějak se v tom motám pořád dokola a nemůžu se ničeho dobrat.

Díky, Lenka

Offline

  • (téma jako vyřešené označil(a) Dale.Lenka)

#2 11. 12. 2012 20:01

Luky_1992
Zelenáč
Příspěvky: 1
Škola: Žilinská univerzita - Elektrotechnika
Pozice: Študent
Reputace:   0 
 

Re: Integrál

Hneď Ti dám riešenie :)

Offline

 

#3 12. 12. 2012 10:26

Dale.Lenka
Příspěvky: 70
Reputace:   0 
 

Re: Integrál

↑ Dale.Lenka:

Už se v tom hrabu několik dní. Včera mě napadla substituce, ale dostala jsem se k $\int_{}^{}\frac{dt}{2t^{2}+1}$ a zase se úspěšně zasekla. Už z toho nevím, čí jsem ... Pomůže mi někdo?

Offline

 

#4 12. 12. 2012 10:42

Brano
Příspěvky: 2655
Reputace:   231 
 

Re: Integrál

Predpokladam, ze si urobila substituciu $t=\tan x$ co je dobre. Teraz este urob $y=\sqrt{2}\;t$ a mas to.

Offline

 

#5 12. 12. 2012 11:09

Dale.Lenka
Příspěvky: 70
Reputace:   0 
 

Re: Integrál

↑ Brano:

To mi vyšlo

$\frac{1}{\sqrt{2}}arctgy=\frac{1}{\sqrt{2}}arctg(\sqrt{2}t)=\frac{1}{\sqrt{2}}arctg(\sqrt{2}tgx)$

Není to nějaký divný?

Offline

 

#6 12. 12. 2012 11:19

rleg
Místo: Ostrava
Příspěvky: 920
Škola: VŠB FMMI (10-16, Ing.)
Reputace:   46 
 

Re: Integrál

↑ Dale.Lenka:
Je to správně

Radim, tedy jsem.

Dobrá rada je drahá, ta moje je zdarma.

Offline

 

#7 12. 12. 2012 12:16

Dale.Lenka
Příspěvky: 70
Reputace:   0 
 

Re: Integrál

↑ rleg:

Díky moc za radu :-)

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson