Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#9 15. 12. 2012 20:49 — Editoval Honza90 (15. 12. 2012 23:54)
Re: kuželová plocha
↑ Brano:
To mě napadl nějaký blud. Myslel jsem na to, že kdyby oba parametry byly ze stejného intervalu, tak by se daly rovnice vyjádřit jen jedním parametrem, ale když jsem si to rozmyslel, tak mi došlo, že to by bylo ve většině případů dost komplikované.
Btw. v maplu to vykresluje pěkně. Ještě jednou díky za pomoc ;)
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline

 a vrchol
a vrchol ![kopírovat do textarea $V=[0,0,1]$](/mathtex/07/077d9588d821939775410bc92db9b0e0.gif) . Díky za pomoc.
. Díky za pomoc. zostroj polpriamku veducu z
zostroj polpriamku veducu z  cez
cez 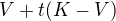 pre
pre 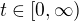 .
.


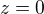
![kopírovat do textarea $V + t(K-V)=[0,0,1]+t[(u,\sin u,0)-(0,0,1)]=(tu,t\sin u,-t+1)$](/mathtex/a6/a68d9984065292e6e3928ea8669f3cae.gif)
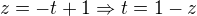
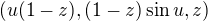
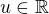 a
a  cize
cize ![kopírovat do textarea $z\in(-\infty,1]$](/mathtex/db/db8ede6b6162317ccaa7932e46760b69.gif) , ak by si bral
, ak by si bral 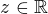 , tak by si tam mal aj opacny "kuzel".
, tak by si tam mal aj opacny "kuzel". ako funkciu
ako funkciu  potom
potom  a
a  ako fciu
ako fciu