Matematické Fórum

PL4 · 16. 12. 2012 21:38

Zdravím, mám tento příklad, nevím, jestli by šlo použít nějaké to L´Hospitalovo pravidlo, ještě jsme to nebrali, takže musím bez něj.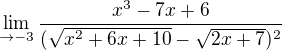

$\lim_{\to-3}\frac{x^{3}-7x+6}{(\sqrt{x^{2}+6x+10}-\sqrt{2x+7})^{2}}$

Zkusím rozšířit tím, co mám ve jmenovateli, takhle: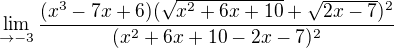

$\lim_{\to-3}\frac{(x^{3}-7x+6)(\sqrt{x^{2}+6x+10}+\sqrt{2x-7})^{2}}{(x^{2}+6x+10-2x-7)^{2}}$

pak bych tedy dosadilo to té delší závorky v čitateli -3, a dole posčítala:

$\lim_{\to-3}\frac{(x^{3}-7x+6)(4)}{(x^{2}+4x+3)^{2}}$

teď roznásobím: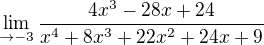
$\lim_{\to-3}\frac{4x^{3}-28x+24}{x^{4}+8x^{3}+22x^{2}+24x+9}$

a vytknu: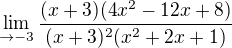

$\lim_{\to-3}\frac{(x+3)(4x^{2}-12x+8)}{(x+3)^{2}(x^{2}+2x+1)}$

no a jsem nahraná, protože po krácení mi dole zbyde závorka (x+3), takže zase nula po dosazení... Můžete mi někdo prosím říct, co je špatně?

Stýv · 16. 12. 2012 22:24

nic není špatně, holt nestačí jenom dosadit (podobně jako je to třeba u limity 1/x v 0)

Bati · 16. 12. 2012 22:38

Zdravím.

Obecně k počítání limit:
Úpravy jsou OK, ale občas zbytečné - např. 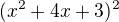$(x^2+4x+3)^2$ si nejdřív rozložím a až pak umocním, ne naopak.
Dále konstanty si můžeš vytýkat před limitu, formálně dokonce musíš, pokud dosazuješ limitní bod do nějaké části limity a předpokládáš, že výsledná limita bude existovat, což se v tomto příkladě právě že neděje, takže nelze jen tak psát čtyřku místo tamtoho výrazu.

PL4 · 16. 12. 2012 22:56

Děkuju za radu ohledně rozložení a až následného umocnění, to mě vůbec netrklo. Když tedy chci něco nahradit, jako v případě té čtyřky, tak to napíšu před limitu, jasné, díky za opravu.
No, ale jsem nahraná dál, protože jestli teď má přijít nějaké to zleva/zprava, tak to vůbec nevím, co s tím. Tohle je první příklad, který zkouším samostatně (ale vypadal z těch daných nejlíp), takže zatím dost tápu, nemůžete mi prosím ještě poradit, nebo třeba odkázat na nějakou stránku, knihu...? Moje poznámky jsou k ničemu:(.

Bati · 16. 12. 2012 23:09

No platí, že limita funkce v nějakém bodě existuje, právě když existují obě limity zprava a zleva daného bodu a jsou stejné.
V tomto příkladě zjistíš, že limita zleva je mínus nekonečno a zprava plus nekonečno, takže se nerovnají a tudíž zadaná limita neexistuje.

PL4 · 16. 12. 2012 23:38

To je trochu demotivující, že hned první příklad, co řeším, nemá limitu:D. Ne vážně, je mi jasné, že když limita zprava = limita zleva, tak limita existuje, jinak ne. Ale nevím, jak zjistím ty samotné limity zleva / zprava. Jak přijdu na to, že je to plus/minus nekonečno? Promiň, jestli je to hloupá otázka, ale já fakt nevím. Našla jsem v sešitě příklad, který se zdá být analogický, takže podle něj:

$4\lim_{\to-3}\frac{(x+3)(x^{2}-3x+2)}{(x+3)^{2}(x^{2}+2x+1)}$

teď zkrátím a dosadím do toho zbytku, kde nebude vycházet nula, spočítám a opět napíšu před limitu: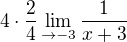

$4\cdot \frac{2}{4}\lim_{\to-3}\frac{1}{x+3}$

takže 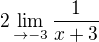$2\lim_{\to-3}\frac{1}{x+3}$

a tohle teď budu nějak řešit dál? Mám tu pak v sešitě v tom podobném případě najednou nějaké nuly se značením + , - v pravém dolním rohu, což jsem pořádně nepochopila, jak se vlatně používá. Když si ale představím graf funkce $\frac{1}{x+3}$ , tak z toho mi už je jasné, že to tak s těmi nekonečny bude, i když nevím, jak to formálně zapsat. Takhle nějak tedy?

Bati · 16. 12. 2012 23:54

Vidím, že máš s těmi zápisy problém, doporučuji nastudovat víc teorii. Např. tady:
http://math.feld.cvut.cz/mt/txtb/5/txc3bb5.htm , speciálně pak
http://math.feld.cvut.cz/mt/txtb/5/txc3ba5b.htm a
http://math.feld.cvut.cz/mt/txtb/5/txc3bb5k.htm

PL4 · 17. 12. 2012 00:15 — Editoval PL4 (17. 12. 2012 00:21)

Moc díky, odkazy vypadají skvěle. Zatím jsem to pročetla jen zběžně, to přiznávám, ale snad už mi trochu svítá, doufám. Nabyla jsem tedy dojmu, že bych teď měla udělat něco takového: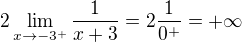

$2\lim_{x\to-3^{+}}\frac{1}{x+3}=2\frac{1}{0^{+}}=+\infty$

a

$2\lim_{x\to-3^{-}}\frac{1}{x+3}=2\frac{1}{0^{-}}=-\infty$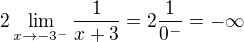

a z toho usoudit, že mám dvě různé limity zprava/zleva a tudíž limita neexistuje?

Bati · 17. 12. 2012 09:00

↑ PL4:
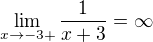Ano, přesně tak, jen pozor na ten zápis $\frac1{0+}$ , někomu by se to nemuselo líbit. Je to jen symbolické a nemá to takhle zapsané žádný matematický smysl, ale můžeš klidně napsat rovnou, že $\lim_{x\to-3+}\frac1{x+3}=\infty$ , to je evidentní.

PL4 · 17. 12. 2012 15:04

Dobře, moc děkuju za pomoc.

Matematické Fórum

#1 16. 12. 2012 21:38

Limita funkce, odmocniny

#2 16. 12. 2012 22:24

Re: Limita funkce, odmocniny

#3 16. 12. 2012 22:38

Re: Limita funkce, odmocniny

#4 16. 12. 2012 22:56

Re: Limita funkce, odmocniny

#5 16. 12. 2012 23:09

Re: Limita funkce, odmocniny

#6 16. 12. 2012 23:38

Re: Limita funkce, odmocniny

#7 16. 12. 2012 23:54

Re: Limita funkce, odmocniny

#8 17. 12. 2012 00:15 — Editoval PL4 (17. 12. 2012 00:21)

Re: Limita funkce, odmocniny

#9 17. 12. 2012 09:00

Re: Limita funkce, odmocniny

#10 17. 12. 2012 15:04

Re: Limita funkce, odmocniny

Zápatí