Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 12. 2012 07:53 — Editoval BakyX (27. 12. 2012 07:54)
Kombinatorická úloha 2
Dobrý deň.
Rád by som nadviazal na úlohu http://www.forum.matweb.cz/viewtopic.php?id=49261 ,a preto pridávam podobnú úlohu. Sami povedzte, či je ťažšia alebo ľahšia :)
Uvažujme množinu 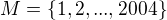 . Nech
. Nech  je ľubovoľná podmnožina
je ľubovoľná podmnožina  s počtom prvkov aspoň
s počtom prvkov aspoň  . Dokážte, že v množine
. Dokážte, že v množine  existujú dva prvky, ktoré môžme označiť
existujú dva prvky, ktoré môžme označiť 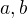 tak, aby platila nerovnosť
tak, aby platila nerovnosť
1^6 - 2^6 + 3^6 = 666
Offline
#2 06. 01. 2014 20:14 — Editoval Brano (06. 01. 2014 20:17)
Re: Kombinatorická úloha 2
Offline

 , tak
, tak . Predpokladajme, ze existuje taka 21 prvkova mnozina
. Predpokladajme, ze existuje taka 21 prvkova mnozina  , ktora splna, ze ak
, ktora splna, ze ak 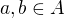 a
a 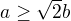 .
. , druhy najmensi je aspon
, druhy najmensi je aspon 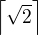 , treti najmensi aspon
, treti najmensi aspon 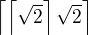 , atd.
, atd.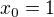 a
a 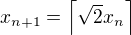 . A mame, ze maximalny prvok
. A mame, ze maximalny prvok 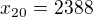 a to je spor.
a to je spor.