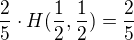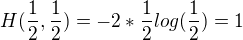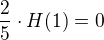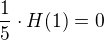Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vzájemná informace (TOTO TÉMA JE VYŘEŠENÉ)
#1 30. 12. 2012 21:12
Vzájemná informace
Ahoj, projíždím příklady z tohoto dokumentu a zasekl jsem se na příkladu č. 3 (Při vysílání dvouprvkové abecedy {., -} se zkreslí 8%...).
Je to sice příkald řešený, ale nedokážu spočítat výslednou vzájmenou informaci dle vztahu I(X; Y) = H(X) - H(X|Y) = 0,725.
Zpětné podmíměné pravděpodobnosti jsem spočítal a vyšli mi  . Správností si jistý vůbec nejsem.
. Správností si jistý vůbec nejsem.
Teorie k této látce se případně nachází v tomto dokumentu.
Děkuji:)
Offline
- (téma jako vyřešené označil(a) darkmagic)
#2 02. 01. 2013 23:01
Re: Vzájemná informace
čísla v matici máš správně, ale myslim, že by součet na řádcích měl být jedna, ale výsledku je to jedno (nevim jak Navarovi), pokud víš co je co a najdeš tam správný data tak ok, já to třeba do matice ani nepsal, jen jsem si pod sebe napsal ty 4 hodnoty
teď je potřeba spočitat ty H(X) a (H(X|Y):
H(X)=-[px(.)log(px(.))+px(-)log(px(-))]=-[0,5log(0,5)+0,5log(0,5)]=1
H(X|Y) na to je vzorec v dalším příkladu, jen si otoč X a Y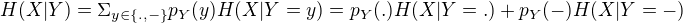
číselně: =0,47*0,1486+0,53*0,38601=0,2744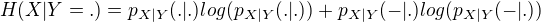
obdobně pro čárku, pak to dosadíš do H(X|Y) a vyjde ti 0,47*0,1486+0,53*0,38601=0,2744
když to odečteš od jedničky, tak ti vyjde 0,7256 - chtělo by to ještě srazit o 0,0002, ale myslim, že to mám dobře
Offline
#3 03. 01. 2013 01:56
Re: Vzájemná informace
Ahoj ↑ honzvit:,
díky za odpověď a zároveň koukám, že tvůj první přspěvěk tady, vítám tě.
Matice s jednotkovým součtem řádků tedy potom  ,
,
ale napsat to jen tak pod sebe má taky něco do sebe, aspoň se to nesplete. I teď mám pochybnost, jestli jsem neprohodil řádky matice.
Postup dále vypadá dobře, jen mám jednu otázku:
ve vztahu pro 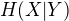 se dosazuje pravděpodobnost
se dosazuje pravděpodobnost 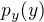 , resp. po dosazení
, resp. po dosazení 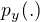 a
a 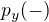 .
.
Pro případ 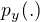 dosadím a mám
dosadím a mám 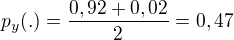 . Proč je tu podíl číslem dvě (prům. hodnota)? Výraz
. Proč je tu podíl číslem dvě (prům. hodnota)? Výraz 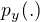 chápu jako pravděpodobnost, že na výstupu bude tečka.
chápu jako pravděpodobnost, že na výstupu bude tečka.
Vidím, že pro čárku by pravděpodobnost vyšla vyšší než 1 a že by to bylo divné.
Mohl by jsi prosím tuto prům. hodnotu podložit nějakou teorií (třeba článek z teorie)?
Offline
#4 03. 01. 2013 11:13
Re: Vzájemná informace
to pY se počítá i v tom Bayesově vzorci pro P_X|Y, kde pod zlomkem v Bayesovi je P(Y), tady je to popsaný pro náš příklad jako suma součinu dvou pravděpodobností a to pro tečku: pst, že byla přijata tečka, za předpokladu, že byla vyslána tečka * pst, že byla vyslána + pst, že byla přijata tečka, za předkokladu vyslání čárky * pst vyslání čárky --- tady se bere to dělení dvěma - pravděpodobnost, že byl vyslán ten daný symbol je 1/2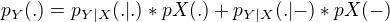
je to docela základní myšlenka z podmíněný pravděpodobnosti
pokud by se v původní zprávě nevyskytovaly symboly 1:1, ale třeba 3:1 víc teček, tak by pY(.) bylo: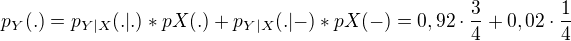
Offline
#5 03. 01. 2013 11:37
Re: Vzájemná informace
↑ honzvit:
Párada, myslím, že jsem tě pochopil. Díky za tvoji pomoc s tímto příkladem.
_________________________________________________________________________________
Měl bych na tebe otázku ještě na příklad 5 z téhož materiálu.
Je tam rychlost entropie Mark. řetezce, která se vypočítá jako střední podm. entropie, tedy jako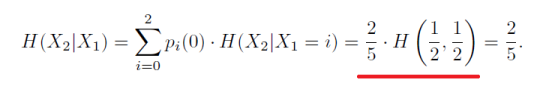 .
.
Mně na tom není jasné to červeně podtrhlé.
Offline
#7 03. 01. 2013 13:20
Re: Vzájemná informace
↑ honzvit:
Mě na tom mate, že v červeně podtrhnuté části výrazu je sdružená entropie a o rovnítko dříve je entropie podmíněná. Jak přejdu ke sdružené?
Offline
#8 03. 01. 2013 15:32
Re: Vzájemná informace
myslim, že náhodná veličina X1 bude řádek a X2 sloupec, pokud máš podmíněnou H(X2|X1=1), tak je to entropie hodnot ve všech sloupcích za předpokladu, že řádek je jedna, takže entropie všech hodnot na prvním řádku, líp ti to nevysvětlim ty materiály moc výřečný nejsou
ještě upozorňuju, že v tom předchozím příspěvku jsem měl chybu, měl jsem tam dvakrát na řádku i=1, teď už je to správně
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vzájemná informace (TOTO TÉMA JE VYŘEŠENÉ)