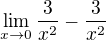Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » limita funkce se sin3x (TOTO TÉMA JE VYŘEŠENÉ)
#2 18. 01. 2013 16:37 — Editoval standyk (18. 01. 2013 16:38)
#5 18. 01. 2013 23:06 — Editoval Emca21 (18. 01. 2013 23:13)
Re: limita funkce se sin3x
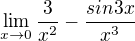
Tahle to ma vypadat?
A je to mysleno tak, ze kdyz 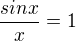 pak take
pak take 
Akorat, ze jsem se ted dival na wolframalfa a tam jim to vyslo
 takze jsem nekde nejspis udelal chybu :-/ Ale uz jsem tak unaveny, ze nedokazu posoudit kde :-/
takze jsem nekde nejspis udelal chybu :-/ Ale uz jsem tak unaveny, ze nedokazu posoudit kde :-/ Miluju veci, kterym nerozumim!
Miluju matematiku!
Offline
#7 18. 01. 2013 23:50
Re: limita funkce se sin3x
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » limita funkce se sin3x (TOTO TÉMA JE VYŘEŠENÉ)